Алгоритм Л.М. Симуни. Оригинальная версия.

Оригинальный и эффективный способ одновременного с полем скорости нахождения градиента давления применительно к стационарным течениям несжимаемой жидкости с переменными теплофизическими свойствами был предложен Л.М. Симуни. Так, используя симметричную аппроксимацию для всех производных по r и односторонние разности для производных оп t и x, можно построить неявную схему, относительно каждой из маршевых переменных, для решения уравнений в Навье – Стокса в цилиндрических координатах в приближении “узкого канала”. В этом случае неизвестные значения сеточной функции 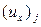определяются из трехточечного уравнения следующего вида:

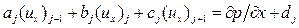. (4.27)

Л.М. Симуни предлагает сеточную функцию 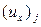представить в виде суперпозиции компонент скорости, опираясь на идею ее физического расщепления:

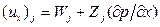. (4.28)

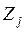При этом сеточные функции и находятся из следующих уравнений:

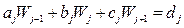; (4.29)

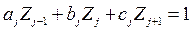; (4.30)

с граничными условиями, обеспечивающие на границах области течения выполнение физических условий для продольной компоненты вектора скорости. Как видно из (4.29), (4.30), функции W и Z находятся независимо от величины 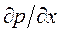. Однако знание градиента давления необходимо при расчете продольной компоненты скорости течения среды по (4.28). Величина 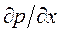определяется из интегрального условия, выражающего собой баланс массы в области течения, расположенной левее выделенного сечения:

, (4.31)

где 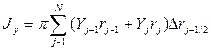, (4.32)

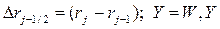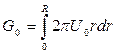; . (4.33)

Здесь 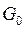– приток среды через входное сечение. После вычисления градиента давления по (4.31) осевая компонента вектора скорости определяется по (4.28), а радиальную компоненты вектора скорости можно получить из конечно-разностного аналога уравнения неразрывности. Далее осуществляется переход к следующему слою по х, а после расчета всего поля течения и к следующему слою по времени.