Уравнение количества движения.

Применение второго закона Ньютона к жидкости, протекающей через бесконечно малый фиксированный контрольный объем, приводит к уравнению количества движения:

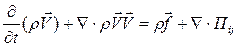. (2.2.1)

Отметим физический смысл слагаемых в левой части (2.2.1). Так, первый член этого уравнения дает отнесенное к единичному объему изменение количества движения в контрольном объеме за единицу времени. Второй член есть отнесенное к единичному объему изменение количества движения в контрольном объеме за счет инерции в единицу времени. Заметим, что 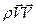– тензор, поэтому 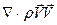не есть просто дивергенция. Однако этот член можно разложить на два слагаемых:

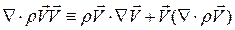. (2.2.2)

Когда это выражение подставляется в уравнение (2.2.1), то, с использованием уравнения неразрывности, последнее упрощается и уравнение количества движения принимает вид:

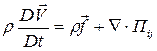. (2.2.3)

Первый член в правой части уравнения (2.2.3) есть отнесенная к единице объема массовая сила. Массовые силы действуют на расстоянии и приложены ко всей массе тела. Чаще всего это – сила тяжести. Второй член в правой части уравнения (2.2.3) дает отнесенные к единице объема поверхностные силы. Эти силы суть механические напряжения, действующие на выделенный жидкий объем со стороны внешней по отношению к нему жидкости. Они образованы нормальными и сдвиговыми напряжениями и задаются компонентами тензора напряжений .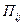

Приведенное выше уравнение выписано для общего случая и пригодно как для течений с разрывами области течения, так и без таковых. Но, как только для тензора напряжений мы принимаем какую-либо аппроксимацию (физическая модель процесса), уравнение (2.2.1) теряет свою общность. Для всех газов, которые можно считать сплошной средой замечено, что напряжение в некоторой точке линейно зависит от скорости деформации жидкости. Такая жидкость называется ньютоновской. При этом допущении можно вывести общий закон деформации, который связывает тензор напряжений с давлением и компонентами скорости. В тензорных обозначениях он записывается в виде:

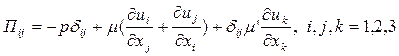, (2.2.4)

где 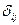– символ Кронекера ( 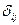=1, если i=j, и 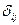=0, если i≠j,); 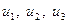– компоненты вектора скорости 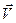; 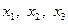– координаты радиус-вектора точки; 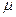– коэффициент динамической вязкости; 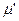– второй коэффициент вязкости. Эти два коэффициента вязкости связаны с коэффициентом объемной вязкости ǽ выражением:

ǽ 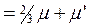. (2.2.5)

Обычно коэффициент объемной вязкости полагают пренебрежимо малым, за исключением тех случаев, когда изучается структура ударных волн, а также поглощением и затухание акустических волн. При ǽ=0 второй коэффициент вязкости станет равным:

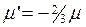. (2.2.6)

а тензор напряжений можно записать как

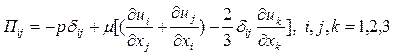. (2.2.7)

Тензор напряжений разделяют часто на две части:

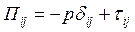, (2.2.8)

где 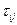– тензор вязких напряжений, задаваемый выражением:

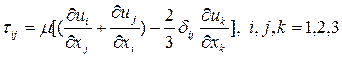. (2.2.9)

Подставляя (2.2.7) в (2.2.3), получаем уравнения движения, которые совместно с уравнением неразрывности (2.1.1) образуют систему, известную как уравнения Навье – Стокса. Итак, уравнения движения имеют вид:

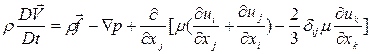. (2.2.10)

Заметим, чтовпервые на основании соображений о взаимодействии молекул эти уравнения были получены Навье в 1822г. и Пуассоном в 1829г. Позднее, используя уравнения динамики сплошных сред (в напряжениях) и уравнение несжимаемости, эти уравнения получил Сен-Венан в 1843г. и затем Стокс в 1845г. Таким образом, уравнения Навье – Стокса образуют базу, на основе которой была развита полная теория вязких течений.

Выше отмечалось, что движение в трубах в технических приложениях носит сложный характер и большей частью оно турбулентно. В таком движении поля скоростей, давлений, температур и других физических величин имеют иррегулярную и очень сложную структуру. Посмотрим на математическое содержание этих процессов.