Алгоритм метода дробных шагов

<78 9 10 11 12 13 >

При построении схем численного интегрирования многомерных уравнений (движения, энергии) используют различные подходы, основанные на представлении разностной схемы в виде последовательности более простых разностных аналогов. Один из таких подходов предложил Яненко Н.Н [13], позднее названный как метод дробных шагов. Он позволяет свести решение сложной задачи к последовательному решению более простых и включает следующие идеи.

1. Геометрическое расщепление, сводящие многомерную задачу к временной последовательности чередующихся задач меньшей размерности или, в частности, к одномерным по пространству задачам. В последнем случае говорят о расщеплении по направлениям.

2. Физическое расщепление, в котором исходный физический процесс представляется в виде чередующейся временной последовательности процессов более простой физической структуры.

3. Аналитическое расщепление, позволяющие на дробных шагах решать различные аналитические задачи, например восстановление дивергентности в схеме предиктор-корректор. При аналитическом расщеплении возможно решение на отдельных дробных шагах аналитическими методами.

Рассмотрим несколько схем расщепления для системы уравнений (4.1) - (4.3).

Схема 1.

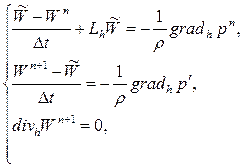(4.34)

где , ,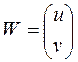

, .

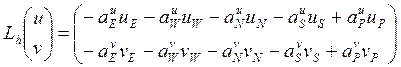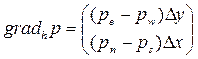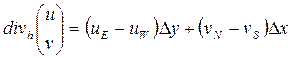Выражая 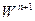из второго уравнения системы (4.34) и подставляя в третье уравнение этой же системы, получим уравнение Пуассона для вычисления поправки давления. Таким образом, алгоритм расщепления, рассмотренный выше, можно представить в виде следующей последовательности этапов:

1. Определение начального поля давления 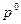и принятие , .

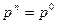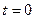2. Задание начального поля скорости .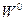

3. Решение уравнений движения для получения .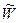

4. Расчет уравнения для 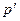и получение 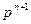путем добавления 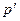к .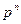

5. Получение 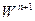с помощью второго уравнения системы (4.34).

6. Принятие .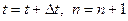

Проверка условия, если t < T_max, то возврат к этапу п.3.

Схема 2.

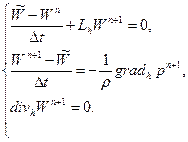(4.35)

Выражая 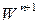из второго уравнения системы (4.35) и подставляя в третье уравнение этой же системы, получим уравнение Пуассона для вычисления давления. Таким образом, данный алгоритм расщепления позволяет представить в виде следующей последовательности шагов:

Задание начального поля скорости .

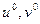Расчет уравнений движения для получения 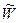(для этого подставляем второе уравнение в первое).

Решение уравнения для .

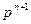Определение 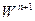с помощью второго уравнения системы (4.35).

Принятие .

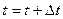Учет условия, если t < T_max, то следует возврат к этапу п.2.

<78 9 10 11 12 13 >

Дата добавления: 2020-07-18; просмотров: 577;