Второе уравнение Фика.

Если стационарное состояние не достигнуто, т.е. концентрация в каждой точке меняется в зависимости от времени, уравнение (1.2) остается справедливым, однако им неудобно пользоваться, поскольку градиент концентрации меняется со временем. Более полезным оказывается другое дифференциальное уравнение, описывающее изменение концентрации диффундирующего вещества в пространстве и во времени. Такая зависимость получается из уравнения (1.2) и баланса вещества.

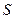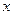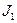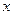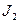Рассмотрим единичную плоскость , расположенную перпендикулярно оси . Пусть - поток вещества через эту плоскость в сечении , а - в сечении 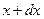(потоки направлены вдоль оси ).

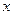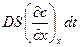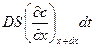Количество вещества проходящего через эти плоскости можно определить из уравнения (1.1)соответственно как и . Количество вещества 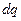накапливающееся в объёме 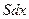за время 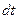с учётом знака в уравнении (1.1) можно определить следующим образом

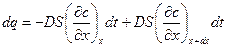(1.3)

Согласно теореме Лагранжа

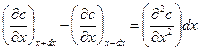
получим

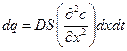(1.4)

Изменение со временем концентрации представляет собой изменение количества вещества в заданном объёме в течении заданного времени, т.е.

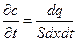
Подставляя в данную запись вместо 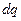уравнение (1.4) получим

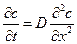(1.5)

это и есть второе уравнение диффузии Фика. Если перейти к трем измерениям, то уравнение (1.5) можно записать в форме уравнения непрерывности для потока

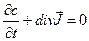(1.6)

Уравнение (1.6) выражает закон сохранения вещества в форме уравнения непрерывности. Если приходится иметь дело с объектами, количество которых не постоянно (например, с вакансиями), то к уравнению (1.6) следует добавить член, равный скорости образования или разрушения этих объектов в единице объема.