Бесконечная система с постоянной концентрацией на поверхности.

Согласно уравнению (1.33) концентрация в плоскости 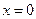для всех времён отжига остаётся постоянной. Это позволяет использовать данное уравнения для области 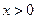в случае, когда из однородного сплава с начальной концентрацией растворенного вещества 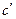происходит его дегазация так, что концентрация на поверхности для всех 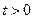поддерживается постоянной равной 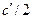. Это можно выразить через следующие граничные условия:

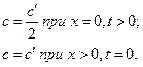
В этом случае решение (1.33) является верным.

Если концентрация на поверхности вместо 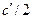равна нулю для всех 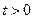, то решение принимает вид:

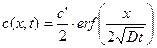. (1.34)

Если на поверхности образца, вначале свободного от растворенного вещества, для последующих всех 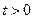, поддерживается постоянное значение концентрации 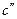, т.е. вещество проникает в образец, то решение для области 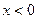эквивалентно предыдущему, поскольку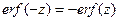

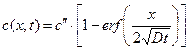. (1.35)

Если исходная или поверхностная концентрация не равна нулю, то в любом из решений уравнений (1.33), (1.34) и (1.35) нулевую концентрацию можно заменить на 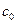. Так если граничные условия:

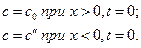
то решение (1.35) меняется на

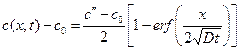. (1.36)