Коэффициент диффузии.

Коэффициент диффузии в уравнениях (1.1) и (1.5) предполагался Фиком, константой, зависящей только от природы диффундирующего вещества, аналогично коэффициенту теплопроводности в уравнении Фурье или коэффициенту удельного сопротивления в законе Ома. На самом деле экспериментально установлено, что коэффициент диффузии зависит от множества параметров, включая концентрацию растворённого вещества и её градиент. Другими словами коэффициент диффузии может изменяться даже в процессе диффузионного отжига.

По своей сути коэффициент диффузии является параметром, характеризующим подвижность диффузанта. Рассматривая движение диффундирующего атома, не следует забывать, что диффузия проходит в кристаллической решётке, где все атомы находятся в постоянном тепловом колебательном движении, и подвижность единичного диффундирующего атома в результате его взаимодействия с окружением может быть различной в разные моменты времени. Говоря о коэффициенте диффузии процесса в целом, имеют ввиду параметр статистический, учитывающий движение не отдельного атома, а всех диффундирующих атомов за достаточно большие промежутки времени.

В сплавах выделяют несколько типов коэффициентов диффузии (коэффициенты гетеродиффузии или химические коэффициенты диффузии).

Так, в случае взаимной растворимости компонент вводится коэффициент взаимной диффузии 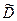. Например, в системе состоящей из компонент 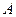и и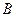х перемешивание происходит за счёт встречных потоков 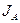и 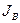. Тот или иной поток относительно неподвижного наблюдателя (например, края образца) должен описываться уравнением диффузии типа

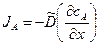, (1.7)

где 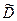- коэффициент взаимной диффузии. Величина 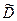зависит от подвижности обоих компонентов и взаимодействия между ними.

Подвижность каждого компонента можно определить через собственный коэффициент диффузии. В области взаимной диффузии, называемой диффузионной зоной плоскости кристаллической решётки возникающего твердого раствора движутся относительно неподвижного наблюдателя в сторону компонента с большим собственным коэффициентом диффузии. В этом случае возникает «течение» решётки как целого. Связь между потоками, например, компонента 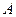в неподвижной ( 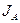) и движущейся ( 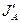) системах координат можно представить следующим образом

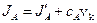, (1.8)

где 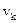- скорость «течения» решетки. Собственный коэффициент диффузии компонента 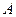относительно неподвижной системы координат можно определить из уравнения для потока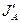

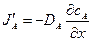(1.9)

Если 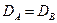, то 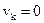и в этом случае 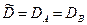. Собственный коэффициент более точно отражает подвижность данного компонента, но не является абсолютно точной величиной, т.к. он зависит от взаимодействия данного компонента с другими и ряда других параметров.

Подвижность какого-либо компонента в многокомпонентной системе можно определить с помощью парциального коэффициента диффузии 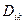из следующего соотношения

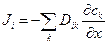(1.10)

Как видно 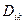представляет собой матрицу, поэтому следует различать диагональные парциальные коэффициенты 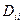и недиагональные 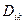. Первые отражают влияние на подвижность 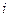-го компонента его же градиента концентрации, а последние – «чужих» градиентов ( ).

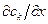Парциальные коэффициенты связаны с собственными следующим выражением

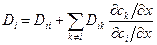(1.11)

Тогда в двойной системе 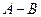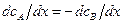и 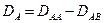. Если 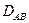мало, то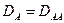

В случае образцов, представляющих собой чистый компонент рассматривают случай градиента изотопной концентрации (концентрации радиоактивных атомов 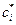). Уравнение Фика принимает вид

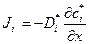(1.12)

где 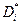- коэффициент изотопной диффузии. Поскольку радиоактивные атомы есть атомы того же элемента, что и матрица, в которой они диффундируют, то 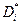- коэффициент самодиффузии. Процесс самодиффузии не обязательно связан с выравниванием изотопного состава. Это могут быть, например, процессы связанные с локальным обменом местами атомом и вакансией.

Помимо упомянутых есть ещё целый ряд коэффициентов диффузии, связанных с процессами миграции атомов по линейным и поверхностным дефектам, по свободной поверхности и т.п. В дальнейшем эти вопросы будут рассмотрены более детально, но сейчас хотелось бы ещё раз обратить внимание на сложный характер понятия коэффициент диффузии.