Бесконечные системы и реальные объекты

В приведенных решениях постоянно присутствует термин «бесконечная или полубесконечная системы». Возникает вопрос имеют ли данные решения практическую значимость? Рассмотрим ещё раз задачу диффузии из бесконечно тонкого слоя в бесконечной системе.

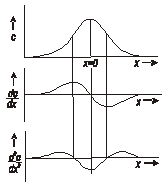
Особенности решения (1.28) проанализируем с помощью графиков, представленных на рисунке 1.2.

На рис 1.2.а представлена зависимость концентрации от длины диффузионного пути. С увеличением времени диффузии ветви кривой 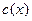распространяются вдоль оси 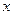симметрично относительно координаты бесконечно тонкого слоя, из которого осуществляется транспорт диффузанта Если количество диффундирующего вещества остаётся постоянным, то площадь под кривой постоянна. Концентрация в точке 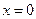уменьшается как 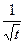, а расстояние между сечением 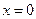и сечением, в котором концентрация в 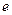раз меньше, растет пропорционально 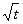. Это расстояния определяется как .

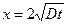Рис. 1.2. Графическое представление решения (1.28)

На рис. 1.2.б представлена зависимость 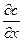от расстояния или ещё говорят от глубины диффузии. Согласно первому уравнению Фика 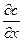пропорционально потоку через любое сечение, отвечающее данному 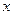. Видно, что при 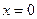поток равен нулю, следовательно, нет переноса вещества через 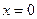из левой части образца в правую и наоборот. На бесконечностях поток так же равен нулю.

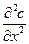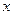На рис. 1.2.в величину отложена зависимость от . Эта величина пропорциональна скорости накопления растворенного вещества в окрестности любого сечения 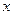. Видно, что в окрестности сечения 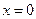кривая вогнута книзу. Это означает, что из данного участка растворенное вещество уходит. Вогнутые кверху участки соответствуют накоплению диффузанта.

Ещё раз напомним, что формула (1.28) есть решение для «бесконечно тонкого слоя», находящегося посередине «бесконечной прямой». Поскольку бесконечности отсутствуют, то следует рассмотреть возможность практического использования данного решения. Если тонкая пленка находится в середине короткого ограниченного участка и вещество без потерь достигает его конца, то в процессе дальнейшего отжига оно должно вначале накапливаться на концах, а затем отражаться внутрь. Тогда значение концентрации растворенного вещества в этом районе должно быть больше по сравнению с тем, которое определяется уравнением (1.28). Таким образом, короткий отрезок можно считать бесконечным, если количество растворенного вещества, которое должно было бы отразиться или находиться вне его в действительно бесконечной полосе, составляет пренебрежительно малую долю от общего количества, растворенного вещества.

Положив 0,1% диффузанта достаточно малой долей, можно найти длину отрезка 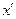, за пределами которого будет находиться эта малая доля

,

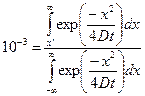где числитель пропорционален количеству вещества, находящемуся далее 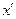на бесконечной прямой, а знаменатель – общему количеству. Числитель, по сути, является функцией ошибок.

Решение этого уравнения 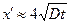, т.е. величина 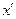зависит от времени отжига 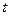. Для достаточно короткого времени любой отрезок является «бесконечным». Длина 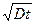появляется во всех диффузионных задачах и «бесконечным» объектом можно считать любой, превышающий по размерам, несколько величин .

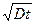Если нанести тонкий слой вещества на один конец образца и дать ему продиффундировать внутрь, то распределение концентрации растворенного вещества описывается уравнением (1.28) для области .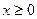

Снимая тонкие слои параллельно исходной поверхности после серии отжигов и измеряя концентрацию диффузанта в каждом снятом слое, можно построить кривую в координатах: 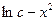. Из уравнения (1.28) следует, что это прямая линия, тангенс угла наклона которой к оси 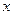равен 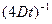. Если известно время отжига 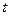, то можно вычислить величину .

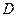Этот способ очень распространен и его часто применяют для всех наиболее точных определений 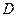атомов замещения.

Сделаем оценку величин из эксперимента, описанного типа. Для атомов замещения в металлах величина 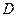вблизи солидуса составляет обычно 10^-8 см²/сек: Чтобы аккуратно найти угол наклона зависимости 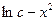, надо снять несколько слоев так, чтобы разбег по концентрациям составлял не менее одного порядка. Это значит, что слои надо снимать до глубины 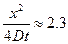или 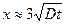. Минимальная толщина слоя, который легко снять на токарном станке составляет около 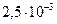см, так что для десяти слоев максимальное значение 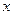составит около 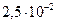см. Если 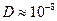см²/сек, то образец длиной 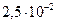см можно считать бесконечным при времени отжига

.

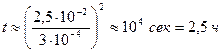Следовательно, выведенные ранее решения для бесконечных систем, вполне применимы для конечных объектов.