Решение для пары полубесконечных твёрдых тел

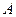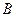Рассмотрим систему, составленную из двух прутков разных веществ и , которые состыкованы по плоскости нормальной оси прутков. Будем считать, что по разные стороны стыка прутки бесконечны. Ограничимся одномерной задачей диффузии вещества из левой части системы в правую. Для решения второго уравнения Фика (1.19) введём следующие граничные условия

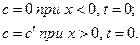
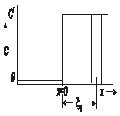
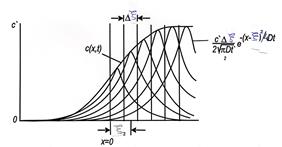
На рис. 1.1 представлен графический образ распределения концентрации в системе.

Рис.1.1 Графическое представление распределения растворённого вещества в начальный момент времени (а) и после отжига (б)

Разобьем область 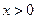на 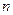участков толщиной 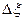. Будем считать, что каждый участок имеет единичную площадь. Каждый участок в момент времени 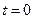содержит 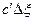растворенного вещества. Рассмотрим один из них. Если бы окружающие участки имели нулевую концентрацию, то распределение 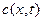после диффузии совпадало бы с решением (1.28) для бесконечного тонкого слоя.

Тот факт, что в окружающих участках есть растворённое вещество, приводит к действительному решению представляющему собой суперпозицию распределений для каждого из участков. Пусть 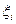– расстояние от центра 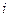–го участка до 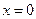. Тогда концентрация в точке 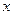в момент времени 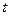определится как

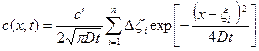. (1.29)

На рисунке 1.б показана сумма экспонент (1.29) дающая истинное распределение для случая относительно толстых участков 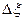. В пределе при 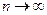, толщины участков 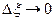и сумма в уравнении (1.29) переходит в интеграл

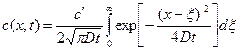. (1.30)

Введём новую переменную 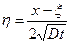, тогда уравнение (1.30) примет вид

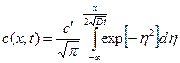. (1.31)

Интегралы такого типа появляются всегда при анализе систем, где есть начальный источник растворенного вещества конечной толщины, а путь диффузии мал по сравнению с размерами системы. Интеграл нельзя просто вычислить, но его значения связаны с функцией ошибок

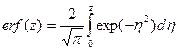. (1.32)

Значения этой функции для различных 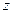сведены в таблицу, которая приведена в приложении 1. Основными свойствами функции ошибок, которыми мы воспользуемся, являются

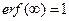и .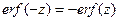

С учётом этого уравнение (1.31) можно записать как:

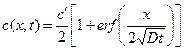. (1.33)

Каждое значение соотношения 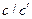связано с определенным значением 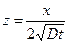. Так, 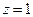всегда соответствует отношению 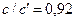, т.е. координата сечения, концентрация в котором составляет 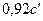, дается соотношением 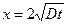. Плоскость с любой постоянной концентрацией удаляется от плоскости 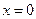со скоростью, пропорциональной 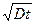. В плоскости 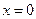для всех времён отжига, отличных от нуля, концентрация остаётся постоянной равной 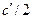. Этой плоскости отвечает 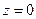и она неподвижна.