Решение для бесконечного стержня.

Рассмотрим одномерный случай, т.е. диффузию в бесконечно длинном стержне. В этом случае граничные условия лишены смысла и можно поставить только начальные. Для постоянного и независимого коэффициента диффузии, второе уравнением Фика для одномерного случая принимает вид:

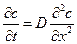(1.19)

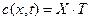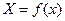Решение этого уравнения можно представить в виде произведения двух независящих друг от друга функций , где - функция пространства, а 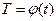- функция времени. Тогда уравнение (1.19) запишется как

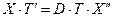
или после разделения независимых переменных

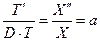, (1.20)

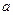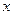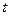где - некая константа, так как и можно менять независимо. Проинтегрируем левую часть уравнения (1.20)

; ; .

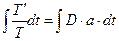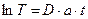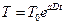Для систем, в которых неоднородность исчезает со временем, т.е. при 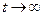, , 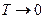необходимо чтобы величина 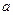была отрицательной.

Обычно полагают 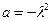, тогда левая часть уравнения (1.20) запишется как:

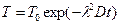, (1.21)

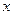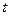но так как и можно менять независимо, уравнение (1.20) будет удовлетворено, только если обе части равны постоянной величине

Правую часть уравнения (1.20) теперь можно записать как

.

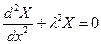Для решения этого уравнения пользуются методом Фурье. Поскольку величина 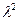всегда положительна, то решение этого уравнения запишется как

.

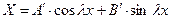Полное уравнение диффузии примет вид

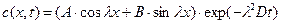, (1.22)

где - , .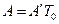

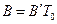Это частное решение. Если оно действительно для любого действительного 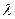, то сумма решений с различными 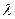тоже есть решение. Общее решение запишется как

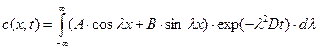. (1.23)

Коэффициенты 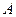и 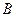можно найти из начальных условий

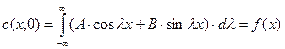. (1.24)

Уравнение (1.24) представляет собой разложение в ряд Фурье, которое можно записать в другом виде:

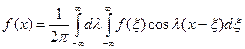(1.25)

или после тригонометрических преобразований косинуса

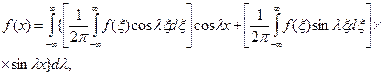
где 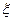- есть некий линейный параметр пространства.

Сравнивая последнюю запись с формулой (1.24) можно увидеть, что коэффициенты 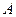и 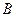соответствуют величинам в квадратных скобках:

;

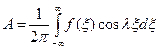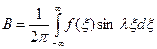
Таким образом, уравнения (1.24) и (1.25) тождественны. Это позволяет нам переписать уравнение (1.23) следующим образом

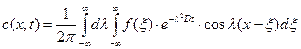
или после перестановки

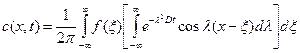, (1.26)

Решим интеграл в квадратных скобках путём замены переменных

.

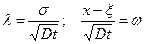Тогда можно записать

.

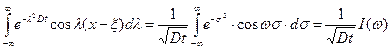При 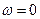интеграл 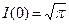- есть интеграл Пуассона. Возьмём производную от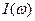

.

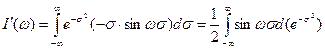Произведём замену переменных

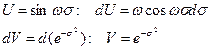
тогда

.

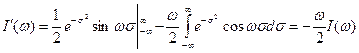Рассмотрим следующее отношение

.

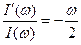После его интегрирования получим

,

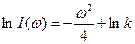где постоянная интегрирования 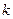= 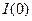. Тогда

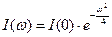или .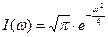

Возвращаясь к прежним переменным 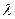и 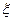общее уравнение диффузии в бесконечном стержне (1.26) запишется теперь как

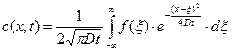
(1.27)

Здесь функция 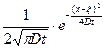обладает свойствами 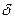функции Дирака, а уравнение (1.27) есть разложение функции координаты 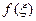по этим 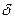функциям.

Представленное решение описывает систему близкую к совершенно однородному распределению, когда выраженного источника диффузии практически нет.