Практический пример

Пусть имеется фирма, состоящая из двух отделов – производственного (П), в задачу которого входит производство некоторого товара, и транспортного (Т), который должен доставить произведенный товар потребителю. Известно, что доход отдела П от выпуска продукции в объеме одной машины равен a денежных единиц, затраты отдела Т на отправку потребителю одной машины с грузом равен c денежных единиц, а затраты на хранение на складе невывезенной продукции в объеме одной машины составляют b денежных единиц и делятся поровну между отделами П и Т.

Пусть также известно, что в интересующий период времени (например за рабочий день) отдел П может произвести продукции в объеме 5 или 10 машин, а отдел Т для ее перевозки выделить малую автоколонну (4 машины), большую автоколонну (7 машин), две малые автоколонны (8 машин) или одну большую и одну малую автоколонны (11 машин).

Моделью описанной ситуации может быть биматричная игра, представленная табл. 4.6.

Таблица 4.6

Тj Пi	Т1(4)	Т2(7)	Т3(8)	Т4(11)
П1 (5 машин)	(4a – b / 2; –4c – b / 2)	(–5a; –7c)	(5a; –8c)	(5a; –11c)
П2 (10 машин)	(4a – 3b; –4c – 3b)	(7a – 1,5b; –7c – 1,5b)	(8a – b; –8c – b)	(10a; –11c)

Необходимо дать рекомендации руководителю отдела П о наиболее выгодном для него объеме производимой продукции (т.е. о выборе стратегии П₁ или П₂), учитывая, что отдел П заинтересован в максимизации своего дохода, а отдел Т – в минимизации своих затрат.

Для получения численных результатов примем a = 10, b = 6, c = 2. Тогда табл. 4.6 примет вид табл.4.7.

Таблица 4.7

Тj Пi	Т1(4)	Т2(7)	Т3(8)	Т4(11)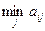
П1 (5 машин)	37; –11	50; –14	50; –16	50; –22
П2 (10 машин)	22; –26	61; –23	74; –22	100; –22

Воспользуемся сначала методом максимина, ориентирующим руководителя отдела П на наиболее осторожное поведение. В этом случае оптимальной является стратегия П₁, гарантирующая отделу П доход в 37 денежных единиц (см. последний столбец табл. 4.7). Учитывая интересы отдела Т (как видно из табл. 4.7, минимальные затраты для Т будут при выборе стратегии Т₁), именно этот доход и будет получен отделом П.

Отметим, однако, что выбор стратегии П₁ вряд ли является наилучшим для отдела П. Так, если он выберет стратегию П₂ и сообщит о своем выборе руководителю отдела Т, то тот, руководствуясь интересами своего отдела, должен будет выбрать стратегии Т₃ или Т₄, что гарантирует доход отдела П в 74 или 100 денежных единиц. Более того, можно «стимулировать» отдел Т на выбор стратегии Т₄, поделившись с ним в этом случае частью дохода, например в 10 денежных единиц (при этом доход отдела П составит 90 денежных единиц, а затраты отдела Т – всего 12 единиц). Именно так скооперировано и рекомендуется действовать руководителю отдела П.

Изменим несколько исходную ситуацию, повысив стоимость хранения не вывезенной продукции: a = 10, b = 10, c = 2. Получим соответствующую таблицу табл. 4.8.

Таблица 4.8

Тj Пi	Т1(4)	Т2(7)	Т3(8)	Т4(11)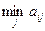
П1 (5 машин)	35; –13	50; –14	50; –16	50; –22
П2 (10 машин)	10; –38	55; –29	70; –26	100; –22

Хотя в этом случае минимально возможный доход для отдела П при выборе стратегии П₁ в 3,5 раза больше, чем при выборе стратегии П₂ (35 и 10 соответственно),однако и в этом случае лучше выбрать стратегию П₂, проинформировав о своем решении руководителя отдела Т. Тот, руководствуясь интересами своего отдела, должен будет выбрать стратегию Т₄ (соответствующую минимальным затратам отдела Т), что гарантирует доход отдела П в 100 денежных единиц. Заметим, что в этой ситуации в «стимулировании» отдела Т нет необходимости.

4.5. Контрольные вопросы к разделу 4

1. Определите игру двух лиц с произвольной суммой.

2. Дайте определение ситуации равновесия в биматричной игре.

3. Сформулируйте теорему 4.1.

4. Приведите примеры биматричных игр, к которым плохо применима теория Нэша.

5. Почему игра типа «семейный спор» объявляется неразрешимой по Нэшу?

6. Определите рефлексивную игру.

7. Кто выигрывает в рефлексивной игре?

8. Рассмотрите практический пример на использование биматричной игры.

9. Рассмотрите в приведенном примере биматричной игры случаи a = 10, b = 6, c = 5 и a = 10, b = 10, c = 5.

5. ОСНОВЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ.
ИГРЫ С «ПРИРОДОЙ»