Практический пример

Снова вернемся к уже рассмотренной ранее (см. п. 3.4) задаче о конкурсе на реализацию двух проектов при участии конструкторских бюро КБ1 и КБ2. Напомним, что у КБ1 (игрока A) имеется 5 стратегий: A₁=(4; 0), A₂=(3; 1), A₃=(2; 2), A₄=(1; 3), A₅=(0; 4); у КБ2 (игрока B) – 4 стратегии: B₁=(3; 0), B₂=(2; 1), B₃=(1; 2), B₄=(0; 3).

Пусть a =16, b =2(т.е. финансированиепервого проекта существенно превосходит финансирование второго проекта).

После приведения данной игры G(5´4)к антагонистической посредством вычитания из выигрышей игрока A средней величины финансирования обоих проектов (a + b) / 2=9, получим ее матричное представление в виде табл. 7.2.

Таблица 7.2

Bj Ai	B1	B2	B3	B4
A1
A2
A3	–7
A4	–7	–7
A5	–7	–7	–7

Далее, после проверки на отсутствие седловой точки и упрощения матрицы игры путем удаления доминируемой стратегии A₅, получим игру G(4´4), представленную табл.7.3.

Таблица 7.3

Bj Ai	B1	B2	B3	B4
A1
A2
A3	–7
A4	–7	–7

В табл. 7.4 приведены результаты, полученные программной системой MatrixGames при использовании приближенного метода Брауна-Робинсона (при задании различного числа итераций) и точного метода Лагранжа (последняя строка таблицы) с округлением результата до трех знаков после запятой.

Из таблицы видно, что некоторая стабилизация для итерационного метода (особенно относительно величины V^*) наступает при числе итераций более 10000.

Таблица 7.4

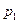
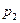
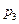
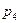
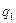
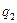
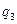
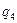
Число итераций									V*
100	0.99	0.01			0.06	0.03	0.93		7.03
200	0,885	0,110	0,005		0,045	0,240	0,485	0,230	7,027
500	0,954	0,044	0,002		0,018	0,096	0,194	0,692	7,009
1000	0,977	0,022	0,001		0,009	0,048	0,097	0,846	7,006
3000	0,905	0,089	0,006	0,003	0,003	0,023	0,175	0,798	7,002
10000	0,895	0,093	0,013	0,001	0,004	0,023	0,180	0,793	7,003
100000	0,879	0,107	0,013	0,002	0,002	0,014	0,111	0,873	7,002
1000000	0,876	0,109	0,013	0,002	0,002	0,013	0,110	0,875	7,002
Точный метод	0,875	0,110	0,013	0,002	0,002	0,013	0,110	0,875	7,002

Вернёмся теперь к исходной задаче. Вычеркнутая стратегия A₅ будет присутствовать в итоговом результате с вероятностью 0:

S_A^*=(0,875;0,110;0,013;0,002;0);

S_B^*=(0,002;0,013;0,110;0,875);

V^* =7,002.

Если теперь вернуться к начальной ситуации с возможным финансированием КБ1 и КБ2 и округлить результаты, то получим:

S_A =(0,9;0,1;0,0;0,0;0,0);

S_B =(0,0;0,0;0,1;0,9);

V_A =16,0;

V_B = 2,0,

Таким образом, КБ1 рекомендуется все усилия направить на выполнение первого проекта, возможно, выделив один отдел на выполнение второго проекта, а КБ2 – наоборот, все усилия направить на выполнение второго проекта, возможно, выделив один отдел на выполнение первого.

7.4. Контрольные вопросы к разделу 7

1. Дайте общее описание программной системы MatrixGames.

2. Поясните структуру главного окна системы MatrixGames.

3. Поясните структуру окна для итерационного метода Брауна-Робинсона.

4. Поясните структуру окна для метода Лагранжа.

5. Поясните структуру окна для метода линейного программирования (симплекс метода).

6. Поясните работу с системой MatrixGames.

7. Рассмотрите практический пример использования системы MatrixGames.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Фон Нейман Д., Моргенштерн О. Теория игр и экономическое поведение: Пер. с англ., М.: Наука, Гл. ред. физ.-мат. лит., 1970, 708 с.

2. Воробьев Н.Н. Теория игр для экономистов-кибернетиков. М.: Наука. Гл. ред. физ.-мат. лит., 1985. – 272 с.

3. Дюбин Г.Н., Суздаль В.Г. Введение в прикладную теорию игр. – М.: Наука, Гл. ред. физ.-мат. лит., 1981, 336 с.

4. Башлыков А.А., Еремеев А.П. Экспертные системы поддержки принятия решений в энергетике / Под. Ред. А.Ф. Дьякова. М.: Издательство МЭИ, 1994, 216 с.

5. Оуэн Г.Теория игр: Пер. с англ., М.: Мир, 1971, 230 с.

6. Воробьев Н.Н. Основы теории игр. Бескоалиционные игры. М.: Наука, Гл. ред. физ.-мат. лит., 1984, 496 с.

7. Нильсон Н. Искусственный интеллект: методы поиска решений: Пер. с англ., М.: Мир, 1973, 270 с.

8. Люгер Д.Ф. Искусственный интеллект: стратегии и методы решения сложных проблем, 4-е издание: Пер. с англ., М.: Издательский дом «Вильямс», 2003, 864 с.

9. Вентцель Е.С. Исследование операций: задачи, принципы, методология. М.: Наука, Гл. ред. физ.-мат. лит., 1980, 208 с.

10. Розен В.В. Цель – оптимальность – решение (математические модели принятия оптимальных решений). М.: Радио и связь, 1982, 168 с.

11. Вилкас Э.Й. Оптимальность в играх и решениях. М.: Наука, Гл. ред. физ.-мат. лит., 1990, 256 с.

12. Ларичев О.И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах: Учебник – 2-е изд., перераб. и доп. М.: Логос, 2002, 392 с.

[1] Программная реализация системы MatrixGames выполнена студентами Ашраповым Д.Ф. и Ашраповой О.В. под руководством старшего преподавателя Чибизовой Н.В.