Случай стохастической неопределенности

В случае стохастической неопределенности предполагаются известными вероятности q_j состояний «природы» П_j, j = 1, …, n. Для поиска оптимального решения применяется критерий Лапласа, согласно которому оптимальной для ЛПР является та стратегия, которая максимизирует средний выигрыш a_i:

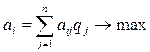
Легко показать, что эта же стратегия будет минимизировать средний риск r_i:

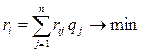
В качестве примера рассмотрим игру, матрицы выигрышей и рисков которой представлены табл. 5.2 и табл. 5.3 соответственно.

Пусть заданы вероятности q_j: q₁=0,1; q₂=0,5; q₃= q₄=0,2.

Тогда:

a₁ = 1·0,1+4·0,5+14·0,2 = 4,9;

a₂ = 3·0,1+8·0,5+7·0,2 = 5,7;

a₃= 4·0,1+6·0,5+8·0,2 = 5.

Согласно критерию Лапласа оптимальной является стратегия А₂.

Расчет относительно рисков также приведет к стратегии А₂:

r₁= 3·0,1+4·0,5+1·0,2 = 2,5;

r₂ = 1·0,1+0·0,5+8·0,2 = 1,7;

r₃ = 0·0,1+2·0,5+7·0,2 = 2.4.

5.2.2. Случай с неизвестными вероятностями
состояний «природы»

Если вероятности состояний «природы» не известны, то для поиска решения ЛПР может применять различные критерии оптимальности. Рассмотрим наиболее используемые критерии.

Критерий Вальда – наиболее осторожный критерий (критерий крайнего пессимизма), согласно которому оптимальной для ЛПР является стратегия, максимизирующая минимальный выигрыш:

.

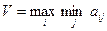Критерий Сэвиджа – также осторожный критерий, согласно которому оптимальной для ЛПР является стратегия, минимизирующая максимальный риск:

.

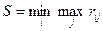Компромиссный критерий Гурвица – компромиссный критерий, согласно которому в качестве оптимальной для ЛПР выбирается стратегия, максимизирующая следующее выражение:

,

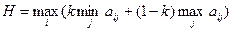где k – коэффициент осторожности (пессимизма), 0 £ k £ 1. Заметим, что при k = 1 критерий Гурвица переходит в критерий Вальда, а при k = 0 имеем так называемый критерий «крайнего оптимизма», предлагающий ЛПР в качестве оптимальной стратегию, максимизирующую максимальный выигрыш.

Естественно, чем ответственнее выбор и чем меньше склонен рисковать ЛПР, тем ближе к 1 следует выбирать коэффициент k. При отсутствии у ЛПР информации для выбора или «по умолчанию» рекомендуется выбирать k » 0,6.

Если ЛПР сомневается при выборе критерия оптимальности, то рекомендуется применить несколько критериев и выбрать ту стратегию, которую рекомендует большинство из них.

В качестве примера рассмотрим игру с «природой», матрицы G(3´4)и R(3´4)которой с некоторыми дополнительными столбцами представлены соответственно табл. 5.4 и табл. 5.5.

Таблица 5.4

G(3´4)

Пj Ai	П1	П2	П3	П4	ai	wi	hi
A1
A2							26,4
A3

Таблица 5.5

G(3´4)

Пj Ai	П1	П2	П3	П4	si
A1
A2
A3

Дополнительные столбцы таблиц содержат следующую информацию, определяемую по соответствующим матрицам выигрышей и рисков: , , , .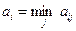

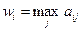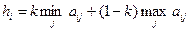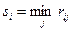Применение соответствующих критериев приведет к следующим результатам:

· согласно критерию Вальда оптимальной для ЛПР стратегией будет A₁;

· согласно критерию Сэвиджа оптимальной для ЛПР стратегией будет A₃;

· согласно критерию Гурвица (с k = 0,6) оптимальной для ЛПР стратегией будет A₃.

Два критерия из трех рекомендуют ЛПР выбрать стратегию A_3., что и следует сделать, если ЛПР не боится риска получить очень маленький выигрыш 11, возможный при выборе этой стратегии. Если такой риск не приемлем для ЛПР, то следует выбрать наиболее осторожную стратегию A₁, рекомендуемую критерием Вальда и гарантирующую минимальный выигрыш 19.

Заметим, что в играх с «природой», как правило, не используются смешанные стратегии по следующим причинам:

· в антагонистических играх смешанные стратегии применяются часто для того, чтобы обмануть, запутать противника, что в играх с «природой» не имеет смысла;

· аппарат смешанных стратегий ориентирован на получение максимального среднего выигрыша, т.е. выигрыша, который будет получен при многократном повторении игры, но в таком случае накапливается статистика и выявляются вероятности q_i состояний «природы», при наличии которых может быть применен критерий Лапласа, дающий решение в чистых стратегиях.

5.3. Контрольные вопросы к разделу 5

· Дайте определение игры с «природой».

· Определите понятие риска.

· Сформулируйте критерий Лапласа для случая стохастической неопределенности.

· Сформулируйте критерий Вальда.

· Сформулируйте критерий Сэвиджа.

· Сформулируйте критерий Гурвица.

· Приведите пример на решение игры с «природой».

· Рассмотрите игру с природой G(4´3), заданную следующей матрицей игры для случая стохастической неопределенности при q₁=0,3; q₂=0,4; q₃=0,1; q₄=0,2 и случая отсутствия вероятностей состояний природы:

Пj Ai	П1	П2	П3	П4
A1
A2
A3

· Дайте пояснения по поводу использования смешанных стратегий в играх с «природой».