Переход к алгебраическим критериям устойчивости непрерывных систем.

Непосредственное вычисление корней характеристического уравнения представляет собой громоздкую операцию. Поэтому важно иметь критерии устойчивости, позволяющие установить факт устойчивости многочлена без вычисления его корней.

Рассмотрим характеристическое уравнение системы

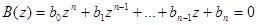(50)

Для оценки устойчивости могут использоваться критерии устойчивости непрерывных систем. Используем преобразование

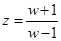, (51)

которое переводит внутренность единичного круга плоскости “z”, в левую полуплоскость плоскости “w”, Rew<0. Действительно, пусть w=u+iv , тогда

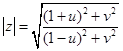
откуда следует, что при 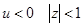, при , при 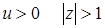. После преобразования (51) характеристическое уравнение (50) принимает вид

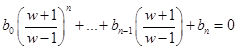
или

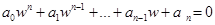, (52)

где коэффициенты 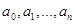выражаются через коэффициенты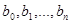

Таким образом, необходимым и достаточным условием устойчивости импульсной системы становится расположение корней 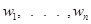уравнения (52) в левой полуплоскости плоскости. Для этого могут использоваться известные критерии устойчивости непрерывных систем (Рауса, Гурвица, Михайлова и др.). Недостатком такого подхода является трудность применения этих критериев для систем высокого порядка из-за громоздких преобразований.

Пример. Пусть характеристическое уравнение системы имеет вид

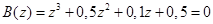
Оценим устойчивость такой системы. С использованием преобразования (51) характеристическое уравнение примет вид

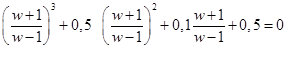
Преобразовав левую часть, окончательно получим

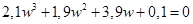
Для оценки расположения корней последнего уравнения применим критерий Гурвица. Составим определитель Гурвица

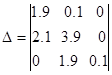
Легко видеть, что 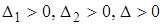( 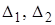- главные диагональные миноры определителя), т.е. импульсная система устойчива.