Спектры сигналов в дискретной системе.

Причина такого изменения спектра с формальной точки зрения становится понятной, если вспомнить связь между изображением решетчатой функции 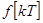и преобразованием Лапласа исходной непрерывной функции. Это известная формула 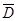- преобразования

.

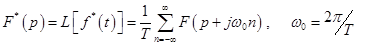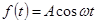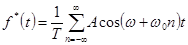Из этой зависимости следует, что если , то , т.е. процесс квантования сопровождается возникновением бесконечного множества дополнительных гармонических составляющих, каждая из которых преобразуется непрерывной частью системы.

Пусть теперь 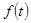- некоторая непрерывная преобразуемая по Фурье функция. Рассмотрим спектр соответствующей решетчатой функции. В соответствии с формулой 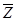-преобразования он определится по зависимости

.

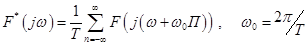Таким образом, частотный спектр 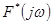включает спектр непрерывной функции при n=0 (основной спектр) и боковые дополнительные спектры, смещенные по оси частот на 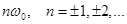(рис. 24). Полезная информация содержится лишь в основном спектре. Если спектр входного сигнала не содержит составляющих c частотой, большей половины частоты квантования, т.е.

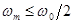, (43)

где 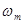- максимальная частота спектра входного сигнала, то боковые спектры не накладываются друг на друга и спектр дискретного сигнала представляет собой простое повторение основного спектра. Тогда, отфильтровывая высокочастотные составляющие 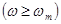, можно восстановить входной непрерывный сигнал из его дискретного представления. Если условие (43) не выполняется, дополнительные спектры перекрываются и восстановление непрерывного сигнала без искажений невозможно. Отметим, что этот результат соответствует теореме Котельникова, рассматриваемой в курсе "Математические основы ТАУ".

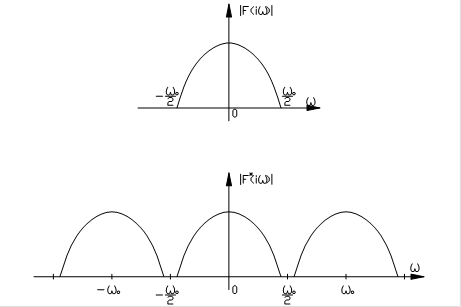Рис.24

Аналогичные рассуждения можно провести и для частотных характеристик дискретных систем. Перепишем зависимость (39)

.

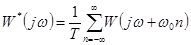Пусть 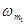-максимальная частота существования АФЧХ приведенной непрерывной части, т.е.

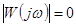при .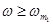

Тогда, если 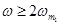, то АФЧХ дискретной системы 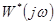имеет вид, аналогичный характеристикам, приведенным на рис.24. Если на вход такой системы подать сигнал, спектр которого удовлетворяет условию (43), то окажется, что выходная величина импульсной САУ будет такой же, как и при подаче соответствующего непрерывного сигнала на вход ПНЧ. В этом случае можно говорить об эквивалентности дискретной системы и ее ПНЧ. Обычно указанные условия выполняются лишь приближенно, при этом спектр непрерывного сигнала при прохождении через дискретную систему искажается. Эти искажения уменьшаются с увеличением частоты квантования 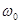, а также при уменьшении частоты 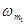, т.е. при улучшении фильтрующих свойств непрерывной части системы. Так как увеличение частот квантования не всегда возможно, то обычно используют второй способ уменьшения искажений передаваемого сигнала. При этом для достижения лучшего эффекта на выходе ИЭ могут включаться дополнительные сглаживающие фильтры. Следует, однако, иметь в виду, что уменьшение полосы пропускания ПНЧ приводит к ухудшению динамики системы, поэтому выбор решения, обеспечивающего хорошую фильтрацию и высокую динамику системы, является сложной задачей. Выше отмечалось, что если 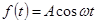, то

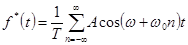. (44)

Из зависимости (44) следует, что даже при малых частотах входного сигнала на вход ПНЧ поступают составляющие высокой частоты 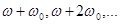, т.е. происходит перенос низкочастотного сигнала в высокочастотную область. В правильно спроектированных САУ ПНЧ фильтрует высокочастотные составляющие и это явление не сказывается на работе системы. Значительно более неблагоприятным оказывается явление переноса высокочастотного сигнала в низкочастотную область. Если на вход системы действует сигнал высокой частоты (например, помеха), то после ИЭ появляются составляющие с частотами 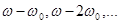Отдельные составляющие этого набора частот могут попасть в полосу пропускания ПНЧ системы, и тогда в замкнутой САУ при высокочастотном входном воздействии возникнут низкочастотные движения, что крайне нежелательно, так как они накладываются на полезный сигнал. Для устранения этого явления следует использовать фильтры, включая их перед импульсным элементом. При этом уменьшается амплитуда помехи, приходящей на импульсный элемент.

Несмотря на то, что АФЧХ дискретной системы не дают полной информации о ее выходном сигнале, они позволяют исследовать устойчивость системы, оценивать качественные показатели САУ, проводить синтез корректирующих устройств. Методы анализа и синтеза цифровых СУ, основанные на использовании частотных характеристик, наиболее часто применяются как инженерные методы расчета таких систем.