Прохождение непрерывного гармонического сигнала через дискретную систему.

Рассмотрим вопрос о прохождении непрерывного гармонического сигнала через дискретную систему. В непрерывной системе входному гармоническому сигналу соответствует выходной гармонический сигнал, т.е. качественного изменения спектра не происходит. Дискретная система изменяет спектр входного сигнала, вводит в него дополнительные составляющие. Приведем простейший пример. Определим реакцию дискретной системы с передаточной функцией 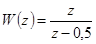на гармонический сигнал 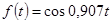. Такую передаточную функцию имеет система, структурная схема которой изображена на рис.22. При этом 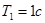, интервал квантования равен 0,693 с и на периоде входного сигнала укладывается 10 таких интервалов.

Используем АФЧХ данной схемы для определения реакции на дискретный сигнал :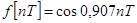

;

.

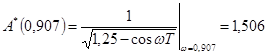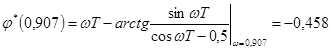Выходной сигнал, рассматриваемый в моменты квантования, имеет вид.

.

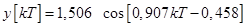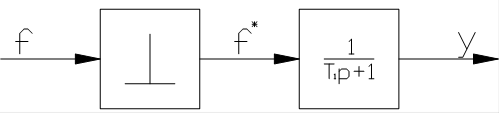Рис.22.

Полученная формула определяет лишь реакцию в дискретные моменты времени, а не вид всего выходного процесса при произвольном времени t. Для построения графика установившегося процесса будем действовать в следующей последовательности:

1. Из последней формулы найдем начальное значение 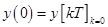, соответствующее данному процессу.

2. На интервале 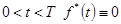. В соответствии с зависимостью для апериодического звена определим выходную величину

,

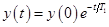при этом

.

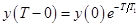3. В момент t=T на вход непрерывной части действует d-функция 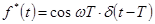. Она вызывает скачок выходной переменной y(t), при этом

.

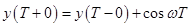В дальнейшем, при 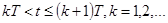процесс вычисления координаты y(t) аналогичен описанному. Внутри каждого интервала выходная величина y(t) имеет вид

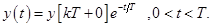
а в точках 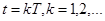сигнал терпит разрыв и при этом

.

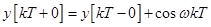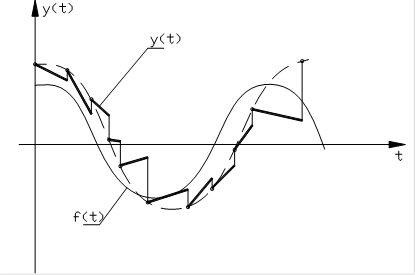График установившегося процесса для рассматриваемой системы приведен на рис.23. Из рисунка видно, что решетчатая функция y[kT], рассматриваемая в моменты квантования, является гармонической. Тем не менее сам процесс гармоническим не является, т.е. дискретная система изменяет спектр входного сигнала.

Рис.23