Условия устойчивости импульсных систем.

Изложим условия устойчивости и линейной импульсной системы, следуя [6] . Рассмотрим полученное ранее уравнение системы во временной области (10)

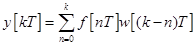
и приведем его к виду

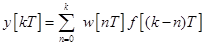. (45)

Пусть внешнее воздействие ограничено, т.е.

.

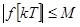Произведем оценку выходного сигнала

.

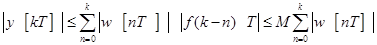Поднимая в последнем неравенстве верхний предел суммирования до бесконечности (это может только усилить неравенство), получим

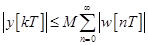. (46)

Очевидно, что импульсная система устойчива, если ряд в правой части (46) сходится, т.е. если

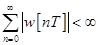. (47)

Таким образом, импульсная система устойчива, если ряд дискрет весовой функции ПНЧ абсолютно сходится. В приведенной формулировке условие (47) является достаточным.

Покажем его необходимость. Положим, что условие (47) не выполняется, т.е.

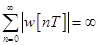. (48)

Тогда можно найти ограниченное входное воздействие, при котором реакция системы будет неограниченной. Пусть при фиксированном k

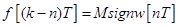
(набор дискрет входного сигнала меняется для каждого). Тогда

.

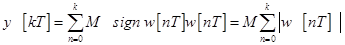Согласно условию (48) для любого наперед заданного числа N всегда можно подобрать такое k , когда

,

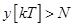что доказывает необходимость условия (48).

Таким образом, условие (48) является необходимым и достаточным условием устойчивости линейной импульсной системы.

Рассмотрим, как оценивается устойчивость линейной импульсной системы по ее передаточной функции. По определению

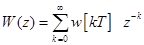
откуда

.

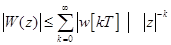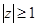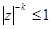Если , то и тогда

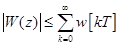при .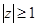

Отсюда следует, что у устойчивой импульсной системы передаточная функция должна быть ограничена в области 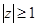, т.е. функция W(z) не должна иметь особых точек-полюсов в области .

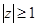Таким образом, импульсная система устойчива, когда все полюсы W(z) удовлетворяют соотношению

,

где n - число полюсов. Случай, когда существуют полюсы 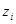такие, что 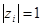, является критическим. Можно показать, что устойчивость обеспечивается, есл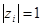и и 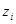- полюс первого порядка передаточной функции W(z) .

Как правило, передаточная функция импульсной системы является дробно-рациональной функцией, т.е.

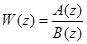
где , A(z) , B(z) -многочлены.

Тогда уравнение

B(z)=0 (49)

будет характеристическим уравнением импульсной системы и для устойчивости необходимо и достаточно, чтобы:

1) все корни уравнения (49) удовлетворяли условию

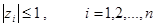
2) корни, модули которых равны единице, были простыми.

Таким образом, на комплексной плоскости z устойчивой импульсной системе соответствуют корни B(z), находящиеся внутри единичной окружности или принадлежащие этой окружности. Асимптотической устойчивости системы, характеризующейся тем, что в отсутствие входного сигнала собственные движения 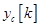стремятся к нулю при 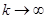, соответствуют полюса передаточной функции, находящиеся внутри единичной окружности

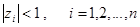
Анализ устойчивости импульсной системы заключается в оценке расположения корней характеристического уравнения на комплексной плоскости.