Анализ устойчивости с помощью критерия Найквиста.

Анализ устойчивости импульсных систем может быть выполнен также с помощью критерия Найквиста, который основан на использовании частотных характеристик разомкнутой системы. Рассмотрим простейшую схему замкнутой системы, представленную на рис.10. Пусть 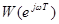- частотная характеристика разомкнутой импульсной системы. Приведем формулировку критерия Найквиста без доказательства.

Пусть характеристическое уравнение разомкнутой импульсной системы имеет l корней вне единичного круга плоскости z. Для того, чтобы была устойчива замкнутая импульсная система, необходимо и достаточно, чтобы годограф 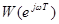при изменении w от 0 до 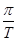охватывал точку 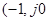) на комплексной плоскости W ровно l/2 раз, т.е.

,

.

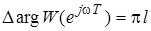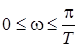Пусть разомкнутая система устойчива. Тогда годограф 1 на рис.26 соответствует системе, устойчивой в замкнутом состоянии, а годограф 2 - системе, неустойчивой в замкнутом виде.

Рис. 26

Случай, когда передаточная функция W(z) разомкнутой системы имеет полюса на единичной окружности плоскости z, относится к числу особых. В этом случае необходимо дополнить годограф частотной характеристики разомкнутой системы дугой бесконечного радиуса аналогично тому, как это делалось при исследовании непрерывных систем. Обычно полюсами, лежащими на единичной окружности, оказываются полюса z=1, что соответствует наличию полюсов p=0 (интегрирующих звеньев) в передаточной функции ПНЧ. При этом годограф АФЧХ разомкнутой системы дополняется дугой бесконечного радиуса, охватывающей столько квадрантов, каков порядок полюса z=1.

Пусть l=0 и разомкнутая система имеет полюс z=1 второго порядка. Годограф АФЧХ, представленный на рис.27а, соответствует системе, неустойчивой в замкнутом состоянии, на рис.27б - системе, устойчивой в замкнутом виде.

Рис.27а Рис.27б.