Критерий Шура-Кона.

Для оценки устойчивости может использоваться также алгебраический критерий Шура - Кона. Рассмотрим характеристическое уравнение (50) и составим из его элементов следующую последовательность матриц:

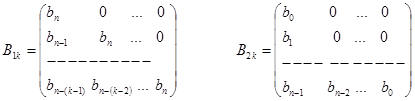
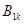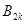Составим из матриц и матрицу 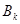размерности (2k´2k)

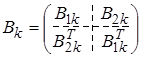, k=1,2,…,n.

Для обеспечения устойчивости импульсной системы с характеристическим уравнением (50) необходимо и достаточно, чтобы число перемен знака в последовательности

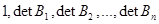
было равно n, т.е. степени характеристического уравнения. Иначе, должно выполняться условие:

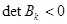для нечетных k ;

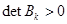для четных k.

Особенностью использования критерия Шура - Кона и его существенным неудобством является необходимость вычисления определителей высокого порядка.

Рассмотрим пример применения критерия Шура – Кона для исследования устойчивости импульсной системы. Пусть характеристическое уравнение системы имеет вид:

.

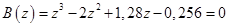Составляем последовательно:

,

,

,

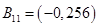
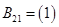
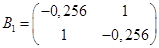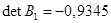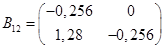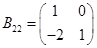
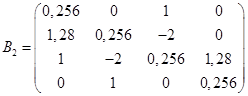
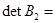0,2841,

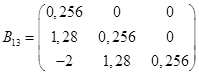
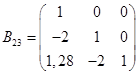
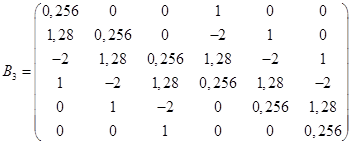
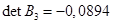
Используя критерий Шура-Кона, можно заключить, что система с данным характеристическим уравнением устойчива.