Алгебраические критерии устойчивости.

Алгебраические критерии устойчивости оперируют с характеристическим многочленом системы. Однако после получения характеристического многочлена перед применением алгебраических критериев нужно убедится в том, что выполняется простое необходимое условие устойчивости. Оно заключается в положительности всех коэффициентов характеристического многочлена и может быть сформулировано следующим образом.

Если автоматическая система устойчива, то все коэффициенты ее характеристического многочлена имеют одинаковые знаки (положительные).

Таким образом, если коэффициенты характеристического многочлена все положительны, то нужно продолжать исследование устойчивости, но, если среди них вместе с положительными имеются и отрицательные, то система заведомо неустойчива.

Докажем это условие. Запишем характеристическое уравнение системы

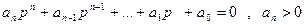(62)

Обозначим корни характеристического уравнения через p₁ , p₂ ,…, p_n. Тогда по теореме Виета имеем

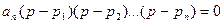(63)

Предположим вначале что все корни вещественные . В устойчивой системе 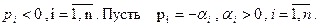Тогда из (63) получим

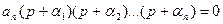
Так как в последнем уравнении все коэффициенты положительны, то, раскрыв скобки мы получим характеристическое уравнение вида (62) с положительными коэффициентами (a_n>0 по исходному положению).

Если в разложении (63) имеется пара комплексно сопряженных корней 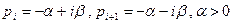, то соответствующая пара примет вид

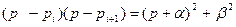
и окончательный вывод о положительности коэффициентов характеристического уравнения сохраняется. Таким образом, необходимое условие устойчивости САУ доказано.

Для систем первого и второго порядка это условие является одновременно и достаточным. Действительно, если характеристическое уравнение первого порядка имеет вид

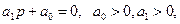
то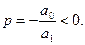

Характеристическое уравнение системы второго порядка имеет вид

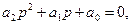
откуда

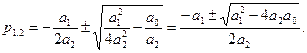
Очевидно, что если все коэффициенты a₀, a₁, a₂ положительны и 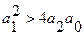, то корни 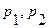действительные и отрицательные. Если 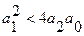, то корни комплексно-сопряженные и .

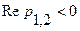Для системы 3-его и более высоких порядков положительность коэффициентов характеристического уравнения является лишь необходимым условием устойчивости.

Критерий Рауса.

В 1868 году Д.К.Максвелл анализируя астатические регуляторы, поставил задачу определения необходимых и достаточных условий отрицательности вещественных частей корней характеристического уравнения. В 1873 году Раус решил ее для уравнений 4-й степени, а в 1877 году он решил эту задачу полностью, сформулировав критерий, носящий его имя.

Рассмотрим характеристическое уравнение системы

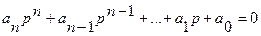
Для удобства изложения перенумеруем коэффициенты, приведя уравнение к виду

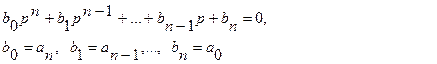(64)

Составим на основе уравнения (64), таблицу, называемую таблицей Рауса.

Коэффициенты с четными индексами				….
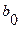
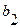
Коэффициенты с нечетными индексами				….
				….
				….
				….
….	….	….	….	….

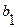
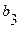
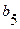
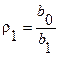
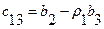
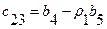
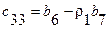
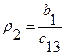
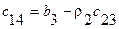
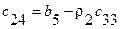
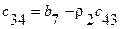
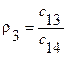
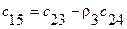
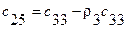
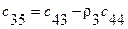
В первой и второй строках таблицы Рауса, начиная со второго столбца, выписываются коэффициенты характеристического уравнения (64) с четными и нечетными номерами. Из чисел верхней строки вычитаются числа нижней строки, помноженные на число 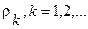, обращающие первую разность такого типа в нуль. Эта нулевая разность не выписывается, остальные разности выписываются в третьей и последующей строках, начиная со 2-го столбца (со сдвигом на один столбец влево по отношению к взятым из верхних строк числам).

Для того, чтобы система была устойчива, необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы Рауса были положительны, т.е.

или, что эквивалентно

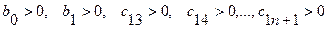
При работе с конкретными числами для упрощения вычислений можно умножать или делить все элементы любой строки таблицы на положительную величину. Это не меняет окончательного результата.

Пример. Оценим устойчивость системы, характеристическое уравнение которой имеет вид

.

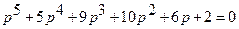Составим таблицу Рауса. Коэффициенты 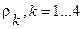положительны. Следовательно, система с таким характеристическим уравнением устойчива.

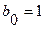
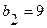
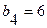
Коэффициенты с четными индексами				Примечания
Коэффициенты с нечетными индексами
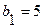
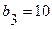
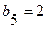
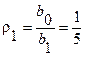
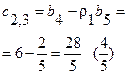
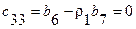
				Делим строку на 7
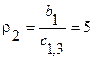
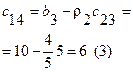
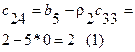
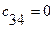
				Делим строку на 2

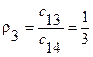
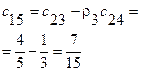
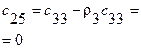
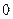
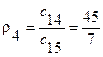
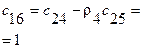
Критерий Гурвица.

В 1895 году, не зная о результате Рауса, Гурвиц разработал и опубликовал алгебраический критерий устойчивости, названный его именем. Критерий Гурвица легко получить из критерия Рауса. Выразим коэффициенты 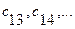через коэффициенты 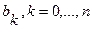характеристического уравнения (64) в виде определителей. Обозначим

.

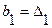Тогда, как можно видеть из таблицы Рауса,

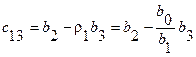
или

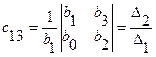
Аналогично

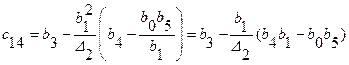
или

.

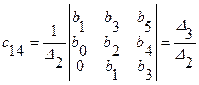Продолжая подобные вычисления, получим

,

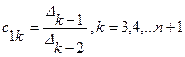где ,-диагональные определители, получаемые из матрицы Гурвица

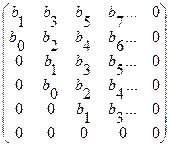
Правило составления матрицы Гурвица. Это (n*n) матрица, записываемая следующим образом.

1.Первая строка составляется из коэффициентов с нечетными индексами, вторая строка – из коэффициентов с четными индексами. Третья пятая и последующие нечетные строки повторяют первую со смещением вправо на один, два, три и т.д. столбца. Аналогичным смещением второй строки формируются четные строки.

2.на главной диагонали матрицы записываются коэффициенты b₁,b₂,…b_n и затем, начиная от диагонального элемента, формируются столбцы: внизу записываются последовательно коэффициенты с убывающими индексами, а вверху – коэффициенты с возрастающими индексами. При выходе за пределы имеющихся крайних коэффициентов b₀, b_n, соответствующие места заполняются нулями.

Критерий устойчивости Гурвица формулируется следующим образом:

Для того, чтобы система с характеристическим уравнением (64) была устойчива, необходимо и достаточно, чтобы определитель матрицы Гурвица (определитель Гурвица) и диагональные миноры этой матрицы были положительны, т.е. чтобы

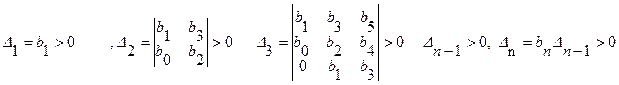
Частным случаем критерия Гурвица является критерий Вышнеградского для системы 3-его порядка. Соответствующее характеристическое уравнение имеет вид

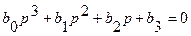
Необходимое и достаточное условие устойчивости для этого случая имеет вид

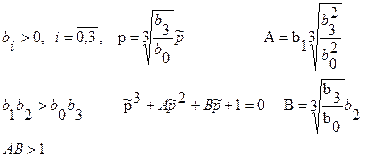
т.е. произведение средних членов характеристического уравнения больше произведения крайних коэффициентов.

В технических приложениях наибольшее распространение получил критерий Гурвица. Для уравнений невысоких порядков этот критерий позволяет получить условия, накладываемые на параметры системы, при выполнении которых САУ являются устойчивой. Однако критерий Рауса легче алгоритмизируется и его проще использовать при анализе устойчивости на ЭВМ.

Пример.

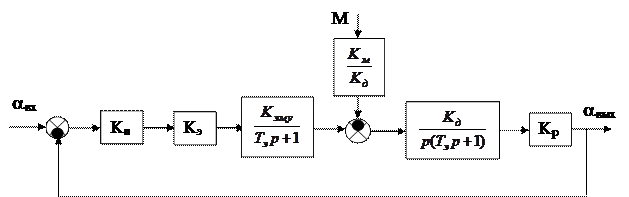Пример. Рассмотрим следящую систему, описываемую уравнениями (14). Соответствующая структурная схема показана на рисунке 56.

Рис.56

Передаточная функция замкнутой системы по входному сигналу имеет вид

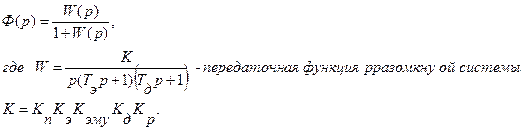
Характеристическое уравнение замкнутой системы имеет вид

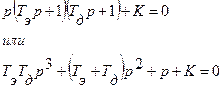
При K>0, T_э>0, T_д>0 условие положительности коэффициентов уравнения выполняются. Составим определитель Гурвица.

.

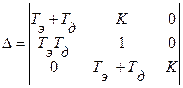Легко видеть, что условие устойчивости принимает вид

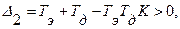
откуда следует неравенство

Условие (66) определяет ограничения, накладываемые на параметры системы. Из него видно, что множество возможных значений коэффициента передачи разомкнутой системы K ограничено сверху значением 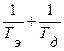. Увеличение K сверх этого значения приводит к неустойчивости системы. Из неравенства (66) видно также, что увеличение постоянных времени ухудшает устойчивость системы, при этом предельное значение коэффициента передачи K уменьшается.