Алгебраические критерии устойчивости

При составлении определителей Гурвица применяются следующие правила:

1. Из коэффициентов уравнения (2.20.) составляется матрица коэффициентов
2. По главной диагонали матрицы выписывают все коэффициенты от a_п-1 до a₀в порядке убывания индекса
3. Дополняют столбцы матрицы вверх от диагонали коэффициентами с последовательно убывающими, а вниз – с последовательно возрастающими индексами
4. В случае отсутствия коэффициента, а также если их индексы больше nили меньше 0, на места коэффициентов ставят нули.

В результате получаем матрицу коэффициентов следующего вида:

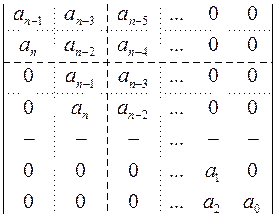(2.24.)

Определители Гурвица составляются на основании матрицы коэффициентов (согласно пунктирным линиям матрицы (2.24.) и имеют следующий вид:

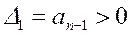(2.25.)

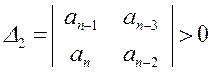(2.26.)

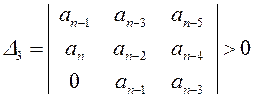(2.27.)

Все последующие определители также должны быть больше нуля. Последний (n-ый) определитель будет включать в себя всю матрицу коэффициентов (2.24.), но обычно его выражают через предпоследний определитель Гурвица (D_n-1):

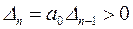(2.28.)

Правильность такого выражения следует из того, что в последнем столбце определителя Δ_nстоят нули, за исключением a₀.

При условии, что все определители Гурвица больше нуля, можно определить границы устойчивости системы. Этого можно достигнуть, приравняв к нулю последний определитель (D_n = 0), а согласно формуле (2.28.) для этого имеется два варианта решения:

1. a₀ = 0 – граница устойчивости первого типа (нулевой корень)

2. D_n-1 = 0 – колебательная граница устойчивости

Недостатками критерия Гурвица являются:

1. Сложность вычислений для уравнений высоких порядков
2. Невозможность определения в неустойчивой системе недостатков, для приведения ее к устойчивой с помощью необходимых изменений.