Аналог критерия Михайлова.

Частотные критерии устойчивости удобно применять к системам высокого порядка. Одним из распространенных критериев устойчивости непрерывных систем является критерий Михайлова. Для импульсных систем можно сформулировать аналог этого критерия.

Пусть характеристическое уравнение замкнутой импульсной системы имеет вид

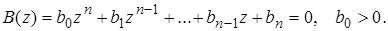
В соответствии с принципом аргумента [3] число корней характеристического многочлена, лежащих внутри единичной окружности, равно числу полных оборотов вектора 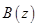при обходе точкой z единичной окружности, т.е.

.

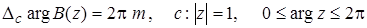Очевидно, что если m = n, то все корни 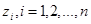удовлетворяют соотношению

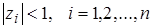
и система устойчива.

Наибольшую сложность при использовании этого критерия представляет нахождение отображения единичной окружности на плоскости B. При этом рассматривать многочлен B(z) в функции z неудобно, так как аргумент z меняется сложным образом. Проще перейти к переменной 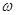по формуле 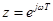. При этом движению точки z по единичной окружности соответствует изменение 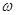в следующих пределах:

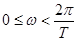
Таким образом, рассматривается функция 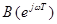и строится ее годограф в пределах 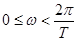. Так как имеет место соотношение

,

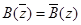то годограф 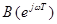при изменении 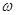в пределах 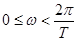симметричен относительно оси абсцисс. Отсюда следует, что можно рассматривать лишь полуветвь годографа, соответствующую половине исходного диапазона 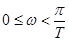. При этом приращение аргумента функции 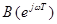также уменьшится вдвое, т.е. ;

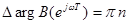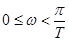
Примеры годографов, соответствующих устойчивым системам при n =1,2, 3, показаны на рис.25.

Рис.25.