Уравнение Ван-дер-Ваальса

1. Точные и приближенные законы. В физике не много законов, которые выполняются точно. Это законы сохранения энергии, импульса, момента импульса и заряда. Большинство же физических законов являются приближенными. Они справедливы лишь тогда, когда значения величин, входящих в формулы законов, лежат в определенных пределах.

2. Отступление реальных газов от уравнения Клапейрона – Менделеева. Уравнение Клапейрона – Менделеева приближенно описывает свойства реальных газов. Оно справедливо лишь при достаточно малых давлениях и выполняется тем точнее, чем ближе подходит газ по своим свойствам к идеальному.

В таблице 8 представлены опытные значения давления p (левый столбец) и объема V (средний столбец), измеренные для 1 моля азотапри температуре 273 К. В правой колонке вычислены произведения pV. Давление p указано в атмосферах (1 атм. = 101 325 Па), а объем в литрах (1 л = 1×10^-3 м³).

Как видно из таблицы 8, произведение pV при больших давлениях не постоянно. Оно растет с увеличением давления p. Реальный газ сжимается меньше, чем это следует из уравнения Клапейрона – Менделеева.

Эти отступления объясняются тем, что молекулы реальных газов, в отличие от частиц идеального газа, имеют собственный объем, который слабо сказывается при малых давлениях. Так при атмосферном давлении среднее расстояние между молекулами примерно в 20 раз больше их диаметра. 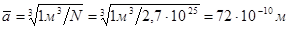. Диаметр молекул азота, например, d = 3×10^-10 м. Отношение ā | d » 72×10^-10| 3×10^-10 = 24.

При давлении в 100 атмосфер среднее расстояние уменьшается примерно в 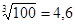раз и составляет около 15×10^-10 м, что лишь в 5 раз больше диаметра молекулы.

Поэтому при больших давлениях вследствие уменьшения расстояния между молекулами роль сил отталкивания и притяжения между молекулами увеличивается настолько, что проявляется не только в момент столкновения, но и между ними.

3. Изотермы Эндрюса. В 1869 г. ирландский исследователь Томас Эндрюс, изучая изотермическое сжатие углекислого газа СО₂ при комнатных и более высоких температурах, обнаружил, что при температурах ниже 31,0°С при достижении определенного давления газ конденсируется и углекислота СО₂ переходит в жидкое состояние. При температурах выше 31,0°С углекислота СО₂ остается в газообразном состоянии при любых сколь угодно высоких давлениях (рис.37).

При температурах t = 13,1°С и 21,5°С с уменьшением объема давление растет монотонно, но при некотором его значении оно перестает увеличиваться и остается постоянным пока газ конденсируется в жидкость. После полного перехода углекислоты в жидкое состояние при дальнейшем сжатии жидкости давление растет очень быстро.

Штриховая линия на графике выделяет область, в которой углекислота находится одновременно в двух состояниях – в жидком и газообразном. Говорят, в двухфазном состоянии. Справа и слева от штриховой линии однофазные области. Справа – газообразное состояние СО₂, слева – жидкое.

Горизонтальные участки изотерм (изобары) в двухфазной области с повышением температуры Т становятся все короче, и при некоторой температуре Т_к, которую Эндрюс назвал критической, изобара вырождается в точку. Для СО₂ Т_к = 31,0°С (304,2 К). Опыты Эндрюса показали, что при температурах, больших критической, газ невозможно превратить в жидкость простым сжатием.

4. Уравнение Ван-дер-Ваальса для 1 моля. Чтобы уравнение состояния идеальных газов могло удовлетворять реальным газам, нужно ввести в него поправки, учитывающие силы взаимодействия между молекулами. Это сделал в 1873 г. голландский физик Иоханнес Ван-дер-Ваальс, предложивший уравнение состояния реального газа для 1 моля в виде:

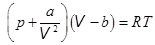. Уравнение Ван-дер-Ваальса, 1873(13.1)

Здесь a и b – поправки, V - мольный объем V = V| v , измеряется в м³| моль. Член a| V ² учитывает дополнительное давление в газах, обусловленное взаимным притяжением между молекулами. Член b – поправка на недоступный для молекул объем, она учитывает силы отталкивания между молекулами.

Уравнение Ван-дер-Ваальса получено в предположении, что b<<V и a| V ²<< p, а молекулы газа симметричны и моделируются твердыми упругими шариками. Не очень плотные реальные газы хорошо описываются уравнением Ван-дер-Ваальса количественно, а плотные лишь качественно. Воображаемый газ, точно подчиняющийся уравнению Ван-дер-Ваальса, называется газом Ван-дер-Ваальса и является идеализацией.

5. Уравнение Ван-дер-Ваальса дляnмолей. С увеличением количества вещества в n раз недоступный объем также увеличивается в n раз и становится равным nb. Уравнение Ван-дер-Ваальса для v молей принимает вид: 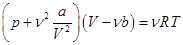. (13.2)

Рассмотрим поправки подробнее.

а. Поправка b. Чтобы оценить поправку b, полагаем, что при каждом акте столкновения двух шаровых молекул для центра любой из них недоступным является объем 4pd ³| 3 (рис.38), где d - диаметр молекул, d = 2r.

Если в сосуде есть N молекул, то недоступный объем при парных столкновениях увеличивается в N| 2 раз и составляет 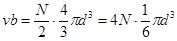. (13.3)

Так как ×pd³|6 есть собственный объем шаровой молекулы, то получается, что поправка nb равна учетверенному собственному объему молекул.

б. Поправка a. Член p_i = n ²a| V ²называется внутренним или молекулярным давлением. Оно обусловлено силами молекулярного притяжения. В отличие от сил отталкивания, действующих на близких расстояниях, силы молекулярного притяжения дальнодействующие. Вид зависимости молекулярного давления p_i от объема V можно установить из следующих рассуждений. Рассмотрим молекулы реального газа вблизи от стенки (рис.39). Если молекула А находится достаточно далеко от стенки и окружена в пределах радиуса R_a действия сил притяжения со всех сторон молекулами газа, то силы притяжения, действующие на нее, со всех сторон одинаковы.

Если молекула В приблизилась к стенке на расстояние меньше R_a, то сила притяжения со стороны молекул газа будет больше, чем со стороны молекул, находящихся между молекулой В и стенкой.

И, наконец, молекула С притягивается только со стороны молекул газа.

В результате молекулы, приближающиеся к стенке, ведут себя подобно телам, брошенным вверх в поле силы тяжести. Их скорость по мере приближения к стенке уменьшается. В результате стенка при ударе молекулы получает меньший импульс, чем тот, который она могла бы получить в начале движения молекулы к стенке.

Внутреннее давление p_i можно определить как давление, действующее на газ, но не доходящее до стенки. Оно пропорционально концентрации молекул газа в пристеночном слое и силе притяжения f, действующей на каждую пристеночную молекулу со стороны молекул газа. Очевидно, эта сила так же пропорциональна концентрации 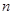, так что p ~ n× f ~ n². Но концентрация обратно пропорциональна объему, n = N| V, n ~ 1| V. Так что p_i ~ 1| V², p_i = a| V ²= n ²a| V ².

6. Межмолекулярное взаимодействие в газах. Может возникнуть вопрос: почему при рассмотрении молекул в пристеночном слое мы пренебрегаем притяжением молекул газа к стенке? Ведь плотность упаковки молекул в стенке больше, чем в газе.

Дело в том, что этот пример с непритягивающейся стенкой использовался лишь как логический метод для выявления роли сил межмолекулярного притяжения. И даже если реальная стенка адсорбирует на своей поверхности часть молекул газа, свойства реального газа, обусловленные силами взаимного притяжения его молекул, не изменятся. Просто прилипание части молекул к стенке приведет к некоторому дополнительному понижению давления из-за уменьшения концентрации свободных молекул.

Силы, действующие между молекулами, электрические по природе. Между молекулами, сблизившимися на расстояние 10^-9 ÷ 10^-10 м, действуют как силы притяжения разноименных зарядов F_прит, так и отталкивания одноименных зарядов F_отт.

Силы отталкивания изменяются с расстоянием быстрее, чем силы притяжения. Если 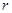- расстояние между центрами двух молекул, то F_отт ~1| r^m, где m » 9 ÷ 15, а F_прит ~ 1| rⁿ, где n » 7. Соответственно быстрее изменяется положительная энергия отталкивания U_отт (рис.40). Суммарная энергия U = U_отт + U_прит имеет минимум U_мин при некотором r₀ (рис.41). У «несклеивающихся» молекул U_мин очень мала по абсолютной величине. Поэтому кинетической энергии молекул при обычных температурах достаточно, чтобы молекулы разлетелись после столкновения.

Положительная энергия отталкивания образуется за счет кинетической энергии движения. После сближения молекул до некоторого расстояния r < r' они вновь расходятся под влиянием сил отталкивания, так что суммарная кинетическая энергия обеих молекул после столкновения оказывается такой же, как и до столкновения.

Правда, это справедливо лишь при низких температурах газа T ≤ 500°С, когда скорости движения подавляющего числа молекул невелики, так что при их столкновении не нарушается внутренняя структура молекул.

При более высоких температурах начинаются процессы диссоциации и ионизации, сопровождающиеся поглощением энергии.