Статистический смысл второго закона термодинамики.

1. Вероятность – это основное понятие статистики. Под вероятностью события понимают величину, обратную числу всех возможных равновероятных исходов.

Пример 1. Грани правильного однородного кубика пронумерованы числами от 1 до 6. Вопрос: какова вероятность того, что кубик при случайном падении встанет на грань №1?

Так как кубик может упасть 6 равноценными способами, то вероятность того, что кубик упадет на грань №1, равна 1/6. Такова же вероятность падения кубика и на каждую из остальных граней.

2. Частота выпадения сумм. Рассмотрим более сложный пример с двумя кубиками.

Пример 2. Определить вероятность выпадения той или иной суммы при одновременном бросании двух кубиков.

При падении кубиков могут наблюдаться следующие ситуации (таблица 7).

Таблица 7

Куб А

Куб В

Сумма S

А

В

S

А

В

S

А

В

S

А

В

S

А

В

S

1

Число всех возможных ситуаций 36. Вероятность появления любой ситуации 1/36. Но число способов реализации ситуации различно (в таблице 7 одинаковые суммы соединены штриховыми линиями).

Сумма å = 2 – 1 способ,

3 – 2 способа,

4 – 3 способа,

5 – 4 способа,

Если бросать кубики много раз, то суммы 6, 7, 8 будут выпадать гораздо чаще, чем 2 или 12, т. к. реализуются большим числом способов. Вероятности их появления больше.

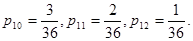Суммы 1, 0, 13 и все другие n > 12 и n< 2 вообще не могут выпасть. Вероятность их появления равна нулю.

Отношению числа реализующих данное событие способов к общему числу всех возможных, называется математической вероятностью события. Очевидно, 0 ≤ p ≤ 1.

3. Термодинамическая вероятность события – это число способов его реализации. В примере 2 W₁ = 0, W₂ = 1, W₃ = 2, W₇ = 6, W₈ = 5, W₁₂ = 1, W₁₃ = 0. Под событием в термодинамике понимается термодинамическое состояние. Если p ≤ 1, то W ≥ 1.

Пример 3. Пусть в сосуде (рис.34) находится 6 пронумерованных молекул. Разделим сосуд мысленно пополам. Число молекул в любой половине может быть от 0 до 6. Вопрос: каким числом способов реализуется каждое состояние?

Состояние, когда в левой половине не будет ни одной молекулы может реализоваться одним единственным способом W₀= 1. Число ситуаций, когда в левой половине одна молекула, равно 6: W₁ = 6. Число ситуаций с двумя молекулами равно числу сочетаний из 6 по 2, то есть 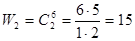. Аналогично для 3, 4, 5, 6 молекул. Число всех возможных комбинаций

W_å = .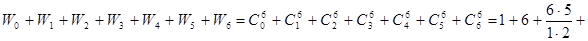

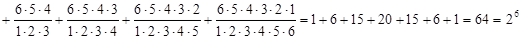Зависимость величины W от числа молекул в одной половине в виде гистограммы на рис. 35.

Если число молекул в сосуде N, то число всех возможных ситуаций W_å =2^N. (12.1)

Говорят, что термодинамическая вероятность W определяет число микросостояний, реализующих данное макросостояние. В примере 3 вероятность равновесного распределения, когда справа и слева одинаковое число молекул, максимальна, W₃ = 20.

4. Второй закон термодинамики в формулировке Больцмана. При большом числе частиц количество способов, которым реализуется равномерное распределение частиц в объеме сосуда, становится подавляюще большим по сравнению с любым другим неравномерным распределением. В ходе непрерывного хаотического движения молекул газ может принимать в принципе любое состояние. Но в подавляющем большинстве случаев мы найдем его в равновесном состоянии, которое реализуется максимальным числом способов и которому соответствует максимальная вероятность W.

Как следует из второго закона термодинамики, изолированная система самопроизвольно переходит в равновесное состояние с максимальной энтропией. Больцман в 1872 г. установил связь между энтропией S и вероятностью W: S = S₀ + klnW, (12.2)

где k = 1,38×10^-23 Дж|К - постоянная Больцмана, S₀ – начальное значение энтропии, W – термодинамическая вероятность. Отсюда, второй закон термодинамики можно сформулировать так: все самопроизвольные процессы в изолированных системах протекают в направлении наиболее вероятного состояния (Л. Больцман, 1872).

Формулировка Больцмана выявляет статистический характер второго закона термодинамики. Статистическое исследование термодинамических систем позволяет установить меру категоричности запрета, налагаемого вторым законом термодинамики.

Пример 4. Найдем вероятность того, что 1 эрг энергии теплового движения молекул перейдет от тела с температурой Т₁ = 301К к телу с температурой Т₂ = 300К. (1 эрг = 10^-7Дж).

Изменение энтропии при равновесном переходе равно

. (12.3)

Здесь Q = 10^-7 Дж, W₂ – термодинамическая вероятность потери теплоты Q нагретым телом Т₁, W₁ – вероятность потери той же теплоты Q холодным телом Т₂. Итак,

.

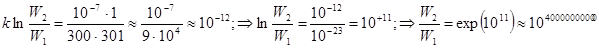Если положить W₁=1, то W₂ = 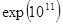. На 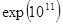переходов 1 эрга энергии от горячего тела к холодному приходится лишь один обратный переход. Таким образом, хотя математическая вероятность антиэнтропийного процесса не равна нулю, но она столь ничтожна, что фактически это эквивалентно запрету.

5. Энтропия – мера беспорядка. Поскольку тепловая энергия тела обусловлена хаотическим движением молекул, а механическая энергия поступательного движения тела представляет собой энергию упорядоченного движения молекул, то ясно, что процесс превращения тепловой энергии в механическую есть, по сути, процесс превращения беспорядочного движения в упорядоченное. Любой беспорядок может быть реализован огромным числом способов, тогда как порядок реализуется, как правило, одним способом. Поэтому энтропия беспорядочного состояния гораздо больше энтропии упорядоченного состояния, а превращение тепловой энергии в механическую сложнее, чем наоборот. Самопроизвольный переход систем в состояние с максимальной энтропией есть, таким образом, переход в состояние максимально возможного беспорядка. Итак, энтропия есть мера беспорядка системы.

6. Демон Максвелла. Максвелл высказал мысль, что в изолированных системах в принципе возможны процессы с уменьшением энтропии, если иметь устройство, пропускающее быстрые молекулы в одну сторону, а другие в другую (рис. 36). Такое устройство, названное по традиции вслед за Лапласом Демоном, без затрат энергии в правой части сосуда соберет быстрые молекулы, а в левой - медленные. В правой части газ будет нагреваться, в левой – остывать. Теплота будет переходить от холодного тела к горячему.

Парадокс разрешается следующим суждением. Сортирующее устройство должно быть молекулярных размеров, а, значит, будет функционировать случайным образом.

Кроме того, перед тем, как «принять решение», открывать или не открывать дверцу перед приблизившейся молекулой, Демон должен измерить ее скорость - послать фотон. По изменению частоты отразившегося фотона Демон мог бы оценить скорость движения молекулы. Но импульс фотона 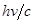соизмерим с импульсом молекулы mv. Поэтому после отражения фотона скорость молекулы изменится и может не соответствовать «решению», принятому Демоном.

Таким образом, как молекулярное сортирующее устройство Демон Максвелла в принципе невозможен.