Исследование уравнения Ван-дер-Ваальса. Критическое состояние в-ва

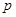1. Графикуравнения Ван-дер-Ваальса в системе координат p,V представляет собой кубическую параболу. На рис.42 показана кривая для 1 моля воды при 373 К. Любому значению давления может соответствовать одно (точки 1 и 3) или три значения объема (точки 2). В двух случаях, когда давление 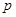соответствует точке максимума c или точке минимума e кривой, из трех значений объема 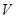два одинаковы.

Уравнение Ван-дер-Ваальса есть уравнение кубическое относительно 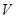. Поэтому значения объемов 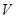в общем случае являются корнями этого уравнения при определенном наборе параметров v, p, T, R, a, b.

2. Сравнение уравнения Ван-дер-Ваальса с уравнением Клапейрона-Менделеева. Преобразуем уравнение к виду, удобному для сравнения: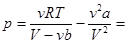

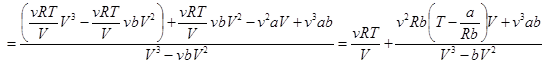(14.1)

Комбинацию констант a| Rb = T_Б называют температурой Бойля.При температуре газа, равной температуре Бойля, Т = Т_Б, числитель дроби принимает минимальное абсолютное значение. Газ при этой температуре ближе всего подходит по своим свойствам к идеальному.

В зависимости от знака разности Т – Т_Б давление реального газа с уменьшением объема изменяется быстрее (Т > Т_Б) или медленнее (Т < Т_Б), чем идеального газа. При Т > Т_Б скобка положительна, давление реального газа растет быстрее, силы отталкивания преобладают над силами притяжения. При Т < Т_Б скобка отрицательна, и если числитель дроби отрицателен, то с уменьшением объема давление реального газа растет медленнее, чем идеального. Силы притяжения преобладают над силами отталкивания.

3. Пересыщенный пар и перегретая жидкость. При совмещении экспериментальной изотермы с теоретической наблюдаются расхождения (рис.43). Проанализируем их, двигаясь по изотерме в направлении сжатия газа (справа налево по рис.43). Участки ab и fg опытной кривой совпадают с изотермой Ван-дер-Ваальса. Участок ab соответствует газообразному состоянию сжимаемого вещества, а участок fg – жидкому.

Состояния, соответствующие участку cde теоретической изотермы в природе существовать по-видимому не могут, так как с уменьшением давления объем вещества не увеличивается, а уменьшается, и наоборот. Поэтому вещество должно находиться здесь в нестабильном состоянии. Оно должно самопроизвольно или коллапсировать в точку e, или раздуваться в точку c.

Участок bc, продолжающий ветвь газообразного состояния ab, соответствует также газообразному состоянию, хотя и несколько ненормальному. Давление газа в любом из этих состояний участка bc больше давления насыщенного пара р_нас.

Такие состояния могут быть реализованы, например, путем быстрого охлаждения тщательно очищенных паров до температуры ниже температуры конденсации. Если нет центров конденсации, пар оказывается пересыщенным. Количество его больше, чем нужно для того, чтобы он был насыщенным.

Состояния, соответствующие участку ef, называются перегретой жидкостью. Их реализовать еще труднее, чем пересыщенный пар. Состояния bc и ef называют метастабильными.

4. Правило Максвелла. Анализ уравнения Ван-дер-Ваальса не позволяет ответить на вопрос: где должна проходить опытная горизонтальная изобара bdf двухфазного состояния системы?

В 1875 г. Джеймс Максвелл указал способ определения положения этой прямой: - так как переход из состояния «b» в состояние «f», независимо от того, будет ли он совершаться по теоретической кривой изотермы, или по опытной изобаре, должен сопровождаться одной и той же работой сжатия вещества, то изобара должна проходить так, чтобы площади криволинейных фигур S₁ и S₂ (рис.44) в системе p,V, были одинаковыми.

5. Критическое состояние вещества. С повышением температуры длина опытной изобары уменьшается и при Т = Т_k вырождается в точку k (Т. Эндрюс, рис.45).

Кубическая парабола уравнения Ван-дер-Ваальса в этой точке испытывает перегиб, то есть имеет экстремум, для которого первая и вторая производные от p по V равны нулю. Используя эти условия, можно найти параметры p_k, V_k и Т_k, соответствующие критическому состоянию вещества.

Уравнение Ван-дер-Ваальса: 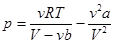. (14.2)

Первая производная от p по V: 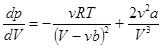. (14.3)

Вторая производная от p по V: 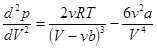. (14.4)

В критической точке получаем систему из трех уравнений с тремя неизвестными p_k, V_k, Т_k.

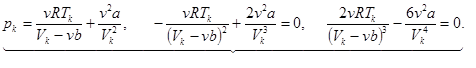(14.5)

Разнеся члены второго и третьего уравнений по разные стороны знака равенства и разделив второе на третье, получаем V_k = 3vb. Из второго уравнения, подставив V_k, получаем: 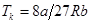. И из первого: 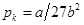. Эти выражения позволяют находить из опытных значений p_k, V_k, Т_k поправки a и b: b=V_k| 3v, 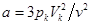. (14.6)

В таблице 9 приведены опытные значения критических параметров p_k, V_k, Т_k некоторых веществ и вычисленные по ним a и b.

В критическом состоянии изобара конденсации вырождается в точку. Это значит, что исчезает переход из газообразного состояния в жидкое и наоборот. При Т > Т_k кинетическая энергия движения молекул больше их энергии связи, поэтому силы молекулярного сцепления не могут удержать вещество в конденсированном состоянии.

Критическое состояние – это не газ и не жидкость. Сжимаемость вещества в критическом состоянии бесконечно велика. 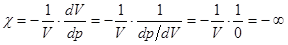. (14.7)

При одном и том же давлении p_k разные области вещества могут сильно отличатся концентрациями частиц. Поэтому вещество в критическом состоянии очень неоднородно. Оптически это проявляется в сильном помутнении обычно прозрачных веществ – критической опалесценции.

6. Пар и газ. Эти термины имеют разный смысл. Пар можно превратить в жидкость изотермическим сжатием, а газ – нет (рис.46). Пар – это газообразное состояние вещества при температуре ниже критической, Т < Т_k. Газообразная вода в атмосфере – это пар (Т_k у воды 374,15°С). А кислород и азот в атмосфере – газы, так как их критические температуры (- 129°С у кислорода и – 147°С у азота) много выше температуры атмосферы. Углекислота СО₂ при Т > 31,1°С – газ, а при Т < 31,1°С – пар.

7. Параметры уравнения Ван-дер-Ваальса a и b, строго говоря, не являются константами. Они заметно изменяются с температурой. Так у аргона, например, при Т = 424 К b = 61×10^{- 6} м³|моль, а = 0,19 Дж×м³|моль². С ростом температуры величины а и b уменьшаются. При Т = 546 К b = 41,0×10^{- 6} м³|моль, а = 0,14 Дж×м³|моль².

Кроме того, опыт показывает, что лучше выполняется условие V_k = 2vb, а не V_k = 3vb. Это говорит о том, что уравнение Ван-дер-Ваальса приближенное, его использование для количественных расчетов требует осторожности.

8. Другие уравнения состояния реальных газов. Из-за недостаточной точности уравнения Ван-дер-Ваальса вскоре стали появляться другие варианты уравнения состояния реальных газов. Отметим два из них.

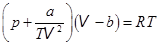. Марселен Бертло. 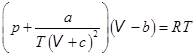. Рудольф Клаузиус

Уравнение Бертло при умеренных давлениях лучше согласуется с опытом, но вблизи критической точки не имеет преимуществ перед уравнением Ван-дер-Ваальса.

Уравнение Клаузиуса лучше соответствует опыту в более широком диапазоне давлений и температур. Но это достигается ценой введения третьей эмпирической константы с, определяемой эмпирически.

9. Измерение критических параметров. В первую очередь определяется критическая температура Т_k. Назовем 3 метода измерений Т_k.

а. Метод Эндрюса, 1869 г. Вещество изотермически сжимается при последовательно повышающихся от опыта к опыту температурах. Постепенно «нащупывается» то значение Т_k, при котором изобара вырождается в точку. Это очень трудоемкий метод.

б. Метод исчезновения мениска, Каньярдела Тур, 1822. Вещество помещается в прозрачную ампулу при температуре ниже критической и нагревается. Если количество вещества мало отличается по критическому объему от объема ампулы, то жидкость при нагревании не испарится, и не заполнит всю ампулу. При достижении Т = Т_k мениск исчезает.

в. Метод А. Надеждина,1885. Пустая металлическая ампула уравновешивалась так, что на горизонтальной оси принимала горизонтальное положение (рис.47-а). После заливки порции вещества ампула поворачивалась вертикально (рис.47-б). В таком положении она нагревалась. Когда температура достигала критической, вещество равномерно распределялось по всему объему, и ампула поворачивалась в горизонтальное положение.

Критическое давление обычно находится изотермическим сжатием вещества при критической температуре по точке перегиба. Молярный критический объем находят чаще всего подбором количества вещества в ампуле.