Средняя длина свободного пробега молекул газа. Явления переноса
1. Столкновения молекул. Впервые детальный разбор явлений столкновения и свободного пробега молекул дал Рудольф Клаузиус в 1858г. Словом "столкновение" молекул мы будем обозначать акт взаимодействия двух молекул, который приводит к заметным отклонением направления их движения от первоначального. При количественном анализе явлений столкновения условие идеальности газа становится менее строгим. Полагаем молекулы уже не материальными точками, а твердыми, абсолютно упругими шариками радиуса r.
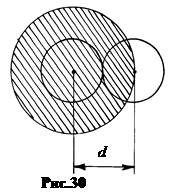
a. Столкновение с неподвижными молекулами. Движущуюся молекулу называют пробной, покоящиеся - полевыми. Полагаем здесь, что полевые молекулы абсолютно неподвижны, движется только пробная. Полевые молекулы ведут себя как частицы с бесконечно большой массой, в результате скорость пробной молекулы при соударении с ними не меняется по величине. Пробная частица при своем движении столкнется в единицу времени со всеми полевыми молекулами, центры которых попадают в объем цилиндра V = s ū, где ū – средняя скорость пробной молекулы, s - ее эффективное газокинетическое сечение. Очевидно, s p (2r)2 = p d 2, где d = 2r – диаметр молекул. На рис.30 сечение s заштриховано. Число столкновений z пробной молекулы в единицу времени равно z = nV = ns ū.  (11.1)
(11.1)
Здесь n – концентрация полевых молекул.
 б. Столкновение с движущимися молекулами. В действительности движутся не только пробная, но и полевые молекулы. Поэтому в формулу должна входить не величина ū, а ūотн, то есть средняя скорость не относительно стенок сосуда, а относительно движущихся молекул. Максвелл показал, что движение полевых молекул увеличивает относительную скорость в
б. Столкновение с движущимися молекулами. В действительности движутся не только пробная, но и полевые молекулы. Поэтому в формулу должна входить не величина ū, а ūотн, то есть средняя скорость не относительно стенок сосуда, а относительно движущихся молекул. Максвелл показал, что движение полевых молекул увеличивает относительную скорость в 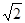 раз. Так что z =
раз. Так что z = 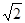 ns ū (11.2)
ns ū (11.2)
Средняя длина свободного пробега молекул есть отношение отрезка пути, пройденного молекулой, к числу соударений, которые молекула испытала на этом пути. Для единичного времени 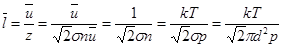 . (11.3)
. (11.3)
В формулу входят два микропараметра s и 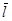 . Чтобы вычислить один из них, другой должен быть найден независимо. Оценим диаметр молекул, предполагая, что в жидком состоянии молекулы упакованы вплотную друг к другу. Тогда на одну молекулу приходится объем, равный отношению молярного объема M|r к числу Авогадро NA. Корень кубический из этого объема дает диаметр молекулы.
. Чтобы вычислить один из них, другой должен быть найден независимо. Оценим диаметр молекул, предполагая, что в жидком состоянии молекулы упакованы вплотную друг к другу. Тогда на одну молекулу приходится объем, равный отношению молярного объема M|r к числу Авогадро NA. Корень кубический из этого объема дает диаметр молекулы. 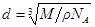 . (11.4)
. (11.4)
Например, для воды H2O M = 18×10-3 кг|моль, r = 103 кг|м3, d =3,1×10-10 м. Средняя длина пробега молекулы водяного пара в воздухе при нормальных условиях. 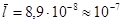 м.
м.
2. Критерий идеальности газа.Чтобы оценить, насколько корректно полагать реальный газ идеальным с невзаимодействующими молекулами, сравним продолжительность столкновения молекул с временем их свободного движения при нормальных условиях. Продолжительность соударения 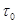 двух молекул есть время пребывания их на расстоянии друг от друга порядка одного молекулярного диаметра, то есть t0 = d/ū. Средняя длина свободного движения есть
двух молекул есть время пребывания их на расстоянии друг от друга порядка одного молекулярного диаметра, то есть t0 = d/ū. Средняя длина свободного движения есть 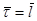 | ū. Так что отношение времен
| ū. Так что отношение времен 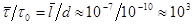 .
.
Итак, столкновения относительно редкое событие в существовании молекулы. Оно в 1000 раз меньше времени свободного движения. Поэтому, реальный газ при обычных условиях (нормальное или пониженное давление, нормальная или повышенная температура) можно считать идеальным, частицы которого не взаимодействуют между собой.
3. Явления переноса – это процессы переноса в пространстве вещества (диффузия), импульса (внутреннее трение), энергии (теплопроводность). Явления переноса существуют во всех средах – в газах, в жидкостях и в твердых телах. При построении их теории плодотворным оказывается понятие средней длины свободного пробега молекул.
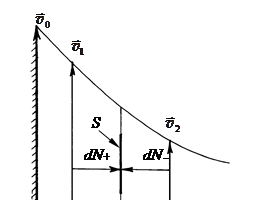
4. Диффузия в газах. Рассмотрим диффузию одного газа в другом. Пусть в газе А есть газ В. Концентрация газа В настолько мала, что его молекулы не сталкиваются между собой, а сталкиваются лишь с молекулами газа А. Найдем поток молекул газа В через воображаемую площадку S в единицу времени (рис. 31). Полагаем массы и размеры молекул А и В одинаковыми. Это позволяет считать скорость ū и среднюю длину свободного пробега 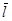 одинаковыми у обоих газов. При таком упрощении диффузию называют самодиффузией.
одинаковыми у обоих газов. При таком упрощении диффузию называют самодиффузией.
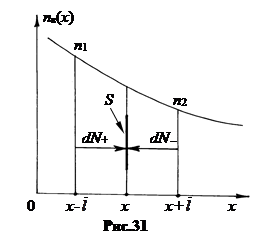 На рис.31 n = n(x) - изменяющаяся вдоль оси ОХ концентрация молекул В,
На рис.31 n = n(x) - изменяющаяся вдоль оси ОХ концентрация молекул В, 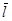 - средняя длина свободного пробега любых молекул. В силу хаотичности движения молекулы диффундируют через площадку S как слева направо (поток dN+), так и справа налево (поток dN-). Но поскольку концентрация молекул В слева и справа разная, то и потоки также разные.
- средняя длина свободного пробега любых молекул. В силу хаотичности движения молекулы диффундируют через площадку S как слева направо (поток dN+), так и справа налево (поток dN-). Но поскольку концентрация молекул В слева и справа разная, то и потоки также разные.
Слева направо, 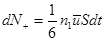 , (11.5)
, (11.5)
Справа налево, 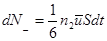 , (11.6)
, (11.6)
Здесь n1 и n2- концентрация молекул В в сечениях 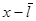 и
и 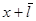 , где x- координата площадки.
, где x- координата площадки.
Суммируем потоки dN = dN+ - dN-= 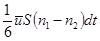 . (11.7)
. (11.7)
Коэффициент 1| 6 обозначает, что при равной вероятности направлений движения молекул вдоль оси ОХ движется треть из них, причем одна половина этой трети движется слева направо, а другая – справа налево.
Число частиц, проходящих сквозь единичную площадку в единицу времени (плотность потока диффузии) есть 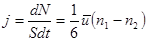 . (11.8)
. (11.8)
Преобразуем 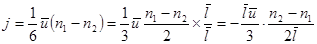 . (11.9)
. (11.9)
Отношение  в силу малости приращения
в силу малости приращения 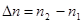 и малости отрезка
и малости отрезка 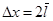 можно записать как производную,
можно записать как производную, 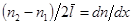 . Обозначив
. Обозначив 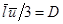 , получаем:
, получаем: 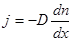 . Закон Адольфа Фика для стационарной диффузии, 1855. (11.10)
. Закон Адольфа Фика для стационарной диффузии, 1855. (11.10)
Выражение dn | dx = grad(n) называют градиентом концентрации. Итак: плотность потока диффузии пропорциональна коэффициенту диффузии D и градиенту концентрации dn | dx. Поток диффузии направлен в сторону понижения концентрации.
| Таблица 4 | |||
| Вещество В | ū м|с | 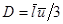 , м2|с
Теория , м2|с
Теория
| D, м2|с Опыт |
| Азот N2 | 0,9×10-5 | 1,7×10-5 | |
| Аммиак NH3 | 1,2×10-5 | 2,0×10-5 | |
| Ацетилен C2H2 | 0,9×10-5 | 1,9×10-5 | |
| Водород H2 | 3,4×10-5 | 6,6×10-5 | |
| Кислород O2 | 0,8×10-5 | 1,8×10-5 | |
| Этиловый спирт C2H5OH | 0,7×10-5 | 1,0×10-5 |
При стационарной диффузии распределение концентрации примесей в пространстве n(x) постоянно во времени. Число частиц В массой m0, диффундирующих за время t через площадку S, равно N = jSt , (11.11)
а масса диффундирующего вещества,
m = m0N = jm0St . (11.12)
В таблице 4 сравниваются вычисленные значения коэффициента диффузии D разных газов, с опытными результатами. Скорость ū вычисляется для молекул вещества В, а длина свободного пробега 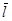 вычислялась для среды – воздуха.
вычислялась для среды – воздуха.
Результаты вычислений совпадают с опытом с точностью до постоянного коэффициента. Вместо числа 1ç3 в формуле D лучше подходит 2ç3, то есть 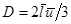 .
.
 5. Вязкость (внутреннее трение). Пусть в однородном покоящемся газе вверх движется гладкая стенка (рис.32) со скоростью v0<<ū. В своем движении стенка увлекает прилегающий к ней слой газа, который, в свою очередь, увлекает следующий слой и так далее. Весь газ как бы делится на тонкие слои, скользящие вверх (по рисунку) тем медленнее, чем дальше они находятся от движущейся стенки.
5. Вязкость (внутреннее трение). Пусть в однородном покоящемся газе вверх движется гладкая стенка (рис.32) со скоростью v0<<ū. В своем движении стенка увлекает прилегающий к ней слой газа, который, в свою очередь, увлекает следующий слой и так далее. Весь газ как бы делится на тонкие слои, скользящие вверх (по рисунку) тем медленнее, чем дальше они находятся от движущейся стенки.
Найдем силу трения между слоями. Каждая моле-кула в слое участвует одновременно в двух движениях – в хаотическом (тепловом) и направленном. Выделим мыс-ленно площадку S, расположенную параллельно слоям. За время dt вправо и влево через площадку проходят одинаковые молекулярные потоки dN+ = dN- = 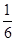 nūSdt. Но эти потоки переносят разный импульс.
nūSdt. Но эти потоки переносят разный импульс.
Слева направо mv1×dN+, справа налево mv2×dN-. Здесь v1 и v2- скорости движения слоев слева и справа от площадки на расстоянии 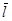 . Разность mv1×dN+ - mv2×dN- есть изменение импульса слоя и должна быть равной импульсу силы трения Fdt, в течении времени dt в направлении
. Разность mv1×dN+ - mv2×dN- есть изменение импульса слоя и должна быть равной импульсу силы трения Fdt, в течении времени dt в направлении  параллельно площадке.
параллельно площадке. 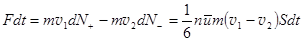 . (11.13)
. (11.13)
Сила трения, действующая на единичную площадку границы соприкосновения двух соседних слоев, есть 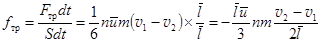 . Максвелл, 1859 (11.14)
. Максвелл, 1859 (11.14)
Отношение 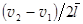 при малости значении величин
при малости значении величин 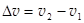 и
и 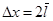 можно записать как производную dv| dx. Ее называют градиентом скорости. Итак
можно записать как производную dv| dx. Ее называют градиентом скорости. Итак
 . Закон Исаака Ньютона, 1687 (11.15)
. Закон Исаака Ньютона, 1687 (11.15)
Величина 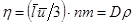 ,h равная произведению коэффициента диффузии D на плотность r называется коэффициентом внутреннего трения или коэффициентом вязкости.
,h равная произведению коэффициента диффузии D на плотность r называется коэффициентом внутреннего трения или коэффициентом вязкости.
Единица измерения h Па×с.
Сила внутреннего трения в газах пропорциональна их вязкости и градиенту скорости.
 Сравнение теоретически найденной вязкости в таблице 5 (четвертый столбец слева) с опытным значением (правый крайний столбец) показывают вполне удовлетворительное соответствие.
Сравнение теоретически найденной вязкости в таблице 5 (четвертый столбец слева) с опытным значением (правый крайний столбец) показывают вполне удовлетворительное соответствие.
6.  Теплопроводность газов. Теплопроводностью называется перенос тепловой энергии в теле при наличии перепада температур. Проанализируем стационарную теплопроводность, когда температуры всех точек в теле сохраняются постоянными.
Теплопроводность газов. Теплопроводностью называется перенос тепловой энергии в теле при наличии перепада температур. Проанализируем стационарную теплопроводность, когда температуры всех точек в теле сохраняются постоянными.
Пусть А и В - две стенки, нагретые до температур ТА и ТВ. Допустим, ТА > ТВ. Между стенками находится газ (рис.33).
Вычислим тепловой поток от стенки А к стенке В. Полагаем, что молекулы, приходящие к площадке слева, обладают средней кинетической энергией 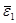 , справа -
, справа - 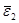 , соответственно температуре газа Т1в сечении
, соответственно температуре газа Т1в сечении  , и температуре Т2 в сечении
, и температуре Т2 в сечении 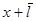 . Суммарный поток энергии через площадку S за время
. Суммарный поток энергии через площадку S за время 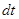 :
: 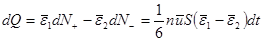 . (11.17)
. (11.17)
Но, 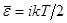 , где i – число степеней свободы молекулы. Тепловой поток через единичную площадку в единицу времени
, где i – число степеней свободы молекулы. Тепловой поток через единичную площадку в единицу времени 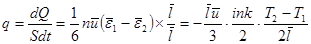 . (11.18)
. (11.18)
Обозначив 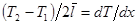 ,
, 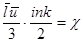 , где c- коэффициент теплопроводности,(11.19)
, где c- коэффициент теплопроводности,(11.19)
получаем: 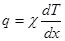 . Закон Фурье для стационарной теплопроводности, 1822(11.20)
. Закон Фурье для стационарной теплопроводности, 1822(11.20)
 Плотность потока энергии q пропорциональна коэффициенту теплопроводности c и градиенту температуры
Плотность потока энергии q пропорциональна коэффициенту теплопроводности c и градиенту температуры 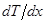 .
.
Единица измерения c Вт|(м×К).
В таблице 6 приведены вычисленные и опытные значения теплопроводности газов при нормальных условиях. Как видно из таблицы, теоретическая теплопроводность удовлетворяет опыту с точностью до коэффициента.
7. Зависимость коэффициентов переноса от давления р и температуры Т. Так как 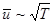 , а
, а 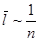 , то
, то 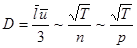 ,
, 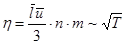 ,
, 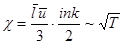 .
.
Коэффициент диффузии D пропорционален 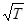 и обратно пропорционален давлению р. вязкость и теплопроводность не зависят от давления. Они растут пропорционально
и обратно пропорционален давлению р. вязкость и теплопроводность не зависят от давления. Они растут пропорционально 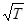 .
.
Дата добавления: 2020-05-20; просмотров: 751;











