Объемные свойства жидкостей
1. Основное отличие жидкостей от газов состоит в том, что жидкости сохраняют свой объем и имеют свободную поверхность. Поэтому свойства жидкостей разделяют на объемные и поверхностные. В этом параграфе рассматриваются объемные свойства.
 2. Сжимаемость. Изотермический коэффициент сжимаемости жидкостей c = -(dV | dp)T | V по сравнению с идеальными газами, для которых c = 1| p, очень мал (Таблица11).
2. Сжимаемость. Изотермический коэффициент сжимаемости жидкостей c = -(dV | dp)T | V по сравнению с идеальными газами, для которых c = 1| p, очень мал (Таблица11).
При нормальном атмосферном давлении p = 105 Па сжимаемость идеальных газов c = 10-5 Па-1. Сжимаемость жидкостей на 5 порядков меньше.
Например, абсолютное уменьшение объема 1 м3 воды по давлением 1 атм составляет DV = cV×Dp = 5,1×10-10×1×105 = 5,1×10-5 м3 =51 см3. Столь незначительное сжатие приводит, тем не менее, к понижению уровня мирового океана на 30 м.
Если перейти в формуле для c к конечным разностям, что допустимо при не очень больших давлениях, при которых c остается постоянной, то можно получить формулу, удобную для практических расчетов. 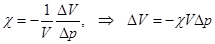 . Если V0 – объем жидкости при некотором давлении p0, то DV = V - V0, где V – объем жидкости при давлении p. Отсюда
. Если V0 – объем жидкости при некотором давлении p0, то DV = V - V0, где V – объем жидкости при давлении p. Отсюда
V - V0 = - c V0 (p - p0); Þ V = V0 [1 -c(p - p0)] . (16.1)
С увеличением давления p коэффициент c уменьшается, и при очень больших давлениях p > 108 Па сжимаемости всех жидкостей становятся практически одинаковыми.
Поскольку с повышением температуры жидкость становится более рыхлой, то нагревание жидкостей приводит к увеличению их коэффициента сжимаемости c.
| Таблица 12 | ||
| Жидкость | Интервал темп-р, °C | b, K-1 |
| Ацетон Вода Глицерин Ртуть Спирт эт. Эфир эт. | -95÷56,5 0÷100 -17÷290 -39÷357 -114÷78 -116÷34 | 1,487×10-3 0,208×10-3 0,505×10-3 0,181×10-3 1,100×10-3 1,650×10-3 |
3. Тепловое расширение. По сравнению с идеальными газами, для которых изобарический коэффициент теплового расширения b = (dV | dT)p| V равен 1/T и при T = 273 К составляет b = 1| 273 = 3,7×10-3 K-1, тепловое расширение жидкостей отличается уже меньше (Таблица 12).
У воды имеется температурная аномалия, состоящая в том, что плотность воды максимальна не в точке замерзания t = 0°C, а при t = 4°C. Дело в том, что молекулы H2O частично ассоциируют в группы (H2O)2, (H2O)3, удельный объем которых различен. При разных температурах соотношение концентраций этих групп разное. При 4°С соотношение ассоциатов таково, что плотность упаковки молекул H2O максимальна. (При t = 0°C r = 999,841 кг/м3, а при t = 4°C r = 999,973 кг/м3).
В общем случае коэффициент b меняется с температурой. Но на линейных участках, где коэффициент b стабилен, в формуле для b можно перейти к конечным разностям.
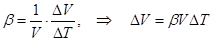 . (16.2)
. (16.2)
Если в качестве отсчетного брать объем V0 при T0 = 273 K, то DT = t°C, и
DV = V - V0 = b V0 t Þ V = V0 =(1 + bt). (16.3)
4. Теплоемкость жидкостей зависит от температуры, причем у разных жидкостей по-разному. У большинства жидкостей с ростом T теплоемкость увеличивается, у некоторых, например, у ртути – уменьшается. Эти колебания теплоемкости могут доходить до 20%.
У воды теплоемкость минимальна при 40°C. При изменении температуры в обе стороны она растет. При t = 0°C c = 4,212×103 Дж/кг×К, при t = 40°C c = 4,174×103 Дж/кг×К, а при t = 100°C c = 4,220×103 Дж/кг×К. Но в целом в диапазоне температур от 0°C до 100°C эти колебания в пределах 1%.
Как и у газов, у жидкостей различают две теплоемкости Cp и CV. Разность Cp - CV = vR также численно равна работе изобарного расширения при нагревании на 1 К. Величина ее у разных жидкостей различна и может быть больше или меньше vR.
 В таблице 13 приведены значения молярной теплоемкости Cp для некоторых жидкостей. Интересно, что у жидких металлов молярная теплоемкость Cp приближается к 3R@25 Дж|(моль×К).
В таблице 13 приведены значения молярной теплоемкости Cp для некоторых жидкостей. Интересно, что у жидких металлов молярная теплоемкость Cp приближается к 3R@25 Дж|(моль×К).
5. Строение жидкостей. Молекулы в жидкостях находятся значительно ближе друг к другу, чем в газах. Если в газах силы межмолекулярного взаимодействия играют заметную роль лишь при низких температурах и значительных давлениях, то в жидкостях эти силы являются преобладающими.
Величина pi = a| V 2 в жидкостях много больше внешнего давления p. Для воды, например, pi = 1,1×109 Па ( = 11000 атм). Поэтому в уравнении Ван дер Ваальса для жидкостей внешними силами можно пренебречь. 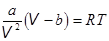 . (16.4)
. (16.4)
Внутреннее давление pi = a| V 2 можно определить путем измерения работы перехода молекул жидкости через поверхностный слой в газ. Такой выход молекул есть процесс испарения, а работа выхода найдется через величину теплоты испарения.
В расположении молекул жидкости наблюдается так называемый ближний порядок. Это значит, что по отношению к любой молекуле расположение ближайших к ней соседей является упорядоченным. Но по мере удаления от данной молекулы нарушения в регулярности накапливаются, и довольно быстро порядок в расположении молекул исчезает. Поэтому жидкости изотропны.
Теория строения жидкостей до сих пор разработана недостаточно и во многих случаях носит полуэмпирический характер. Согласно Якову Френкелю, разрабатывавшему теорию жидкого состояния в 30-х годах 20 в., каждая молекула колеблется около своего положения равновесия. Время от времени молекула меняет место равновесия, скачком перемещаясь в новое положение, отстоящее от прежнего на расстояние порядка диаметра молекул.
Среднее время пребывания молекул в одном месте различно у разных жидкостей и уменьшается с ростом температуры T. Чем выше T, тем чаще перескакивают молекулы. Поэтому с ростом T в жидкостях увеличивается коэффициент диффузии и уменьшается вязкость.
С увеличением T растет средняя энергия теплового движения молекул. Это проявляется в увеличении амплитуды колебания молекул около положения равновесия. Среднее расстояние между центрами молекул с ростом температуры T также увеличивается. Жидкость разрыхляется, ее объем растёт, плотность уменьшается.
6. Диффузия в жидкостях. В газах коэффициенты переноса определяются длиной свободного пробега молекул 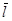 . Но в жидкостях понятие длины свободного пробега молекул теряет смысл. Расстояние межмолекулярного скачка в жидкостях много меньше величины
. Но в жидкостях понятие длины свободного пробега молекул теряет смысл. Расстояние межмолекулярного скачка в жидкостях много меньше величины 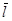 в газах. Поэтому и коэффициент диффузии в жидкостях много меньше, чем в газах.
в газах. Поэтому и коэффициент диффузии в жидкостях много меньше, чем в газах.
| Таблица 14 | |||
| Диффундирующее вещество | Среда | T, K | D, м2/с |
| Газ H2 Сахар C12H22O11 Соль NaCl Золото Au тв. | Газ O2 Вода жидк. Вода жидк. Свинец Pb тв. | 273 293 | 0,7×10-4 0,3×10-9 1,1×10-9 4×10-14 |
В таблице 14 сравниваются коэффициенты диффузии, измеренные в трех средах – в газах, в жидкостях и твердых телах. Величина D в жидкостях на 5 порядков меньше, чем в газах, а в твердых телах на 5 порядков меньше, чем в жидкостях.
По Френкелю, коэффициент диффузии в жидкостях растет с температурой T по закону D = B×exp(- w| kT). (16.5)
 Здесь B – параметр, зависящий от свойств жидкости, w – энергия, необходимая для скачка молекулы (энергия активации), w @ (2 ¸ 3)×10-20 Дж, k = 1,38×10-23 Дж/K – постоянная Больцмана.
Здесь B – параметр, зависящий от свойств жидкости, w – энергия, необходимая для скачка молекулы (энергия активации), w @ (2 ¸ 3)×10-20 Дж, k = 1,38×10-23 Дж/K – постоянная Больцмана.
7. Теплопроводность. Плотность упаковки молекул жидкости примерно на 3 порядка больше плотности упаковки молекул газа. Но примерно во столько же раз расстояние скачка молекул жидкости меньше длины свободного пробега молекул газа. Поэтому коэффициенты теплопроводности газов и жидкостей-диэлектриков отличаются в пределах 1 порядка (Таблица 15).
Как видно из таблицы, теплопроводность жидкостей, обладающих электронной проводимостью (жидкие металлы) на 1-2 порядка больше теплопроводности жидкостей-диэлектриков.
С ростом температуры теплопроводность жидкостей уменьшается. У многих жидкостей эта зависимость c от T приближается к линейной. c = cпл [1 - a(t - tпл)]. (16.6)
Здесь cпл – теплопроводность жидкости в точке плавления tпл, a – коэффициент.
При опытном измерении теплопроводности жидкостей одной из важных задач является устранение конвекции. Обычно это достигается нагреванием жидкости сверху. Тогда легкие слои находятся вверху, более тяжелые – внизу. Подавлению конвекции способствует и уменьшение толщины слоя жидкости, через который проходит тепловой поток.
8. Вязкость жидкостей по сравнению с газами очень велика и быстро уменьшается с ростом температуры (Таблица 16).
| Таблица 16 | |||||
| Жидкость | t, °C | h, мкПа×с | Жидкость | t, °C | h, мкПа×с |
| Ацетон Вода Глицерин Спирт этиловый | -20 +20 +20 -20 +20 +200 -20 +20 | 134×106 1499×103 | Эфир этиловый Алюминий Олово Ртуть Свинец | +20 +661 -20 |
 По Френкелю, вязкость жидкостей с ростом температуры T уменьшается по закону:
По Френкелю, вязкость жидкостей с ростом температуры T уменьшается по закону:
h = A×exp(w| kT)., (16.7)
где A – параметр, зависящий от свойств жидкости.
Русский физик Алексей Бачинский предложил в 1912 г. формулу, в которой зависимость вязкости от температуры выражается в неявном виде через объем жидкости, 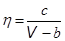 . (16.8)
. (16.8)
Здесь V – молярный объем жидкости, b – постоянная Ван-дер-Ваальса, c – параметр, зависящий от свойств жидкости.
С ростом температуры вязкость жидкостей уменьшается, а вязкость равновесных паров растет. Если на одном графическом поле показать вязкость жидкости и ее равновесных паров, то в критической точке обе кривые сходятся (рис.52).
Сжатие жидкости приводит к росту вязкости. Например, увеличение давления от 1 до 20000 атмосфер приводит к увеличению вязкости воды на 6 порядков.
С понижением температуры вязкость жидкостей растет. Однако в 1938 г. Петр Капица открыл исключение из этого правила. Оно состоит в том, что вязкость жидкого гелия с приближением его температуры к абсолютному нулю не только не увеличивается, но полностью исчезает.
Это явление называют сверхтекучестью жидкого гелия. Оно имеет квантовую природу.
 §17. Поверхностные свойства жидкостей
§17. Поверхностные свойства жидкостей
1. Поверхностный слой. Рассмотрим силы, действующие на молекулу жидкости в глубине ее и в плоском поверхностном слое (рис.53).
Силы притяжения, действующие на молекулу B со стороны окружающих молекул, в среднем одинаковы по всем направлениям.
Этого нельзя сказать о силах притяжения, действующих на молекулу А поверхностного слоя. Силы, действующие в плоскости поверхности, приблизительно одинаковы. Поэтому молекула А в плоскости поверхности находится в безразличном равновесии. Но силы притяжения со стороны молекул жидкости, лежащих ниже молекулы А , много больше сил притяжения со стороны молекул газа, лежащих выше молекулы А . Поэтому молекула А в целом притягивается к массе жидкости. И в таком положении находится каждая молекула поверхностного слоя.
 Благодаря разнице в силах притяжения со стороны молекул жидкости и со стороны молекул газа формируется поверхностный слой жидкости, отделяющий жидкое состояние вещества от газообразного. Поскольку каждая молекула поверхностного слоя притягивается нижерасположенными молекулами жидкости, то она смещается по направлению к молекулам жидкости до тех пор, пока силы притяжения не уравновесятся силами отталкивания (рис.54).
Благодаря разнице в силах притяжения со стороны молекул жидкости и со стороны молекул газа формируется поверхностный слой жидкости, отделяющий жидкое состояние вещества от газообразного. Поскольку каждая молекула поверхностного слоя притягивается нижерасположенными молекулами жидкости, то она смещается по направлению к молекулам жидкости до тех пор, пока силы притяжения не уравновесятся силами отталкивания (рис.54).
Поверхностный слой как бы подпрессовывает жидкость в целом и обладает избыточной по сравнению с остальной массой жидкости энергией. Эту энергию называют поверхностной. Силы притяжения между молекулами поверхностного слоя вызывают стремление жидкости сократить свою поверхность.
 Переход молекулы из глубины жидкости в поверхностный слой требует совершения работы против действующих в поверхностном слое сил. Эта работа совершается за счет кинетической энергии молекул. Поскольку молекулы жидкости обладают разной кинетической энергией, то среди молекул поверхностного слоя всегда найдутся такие, энергия которых достаточна для совершения работы по преодолению Вандерваальсовых сил притяжения. В результате молекула может перейти в газ. Поэтому поверхностный слой не мономолекулярен. Он разрыхлен тем больше, чем дальше находятся молекулы от основной массы жидкости (рис.55).
Переход молекулы из глубины жидкости в поверхностный слой требует совершения работы против действующих в поверхностном слое сил. Эта работа совершается за счет кинетической энергии молекул. Поскольку молекулы жидкости обладают разной кинетической энергией, то среди молекул поверхностного слоя всегда найдутся такие, энергия которых достаточна для совершения работы по преодолению Вандерваальсовых сил притяжения. В результате молекула может перейти в газ. Поэтому поверхностный слой не мономолекулярен. Он разрыхлен тем больше, чем дальше находятся молекулы от основной массы жидкости (рис.55).
2. Поверхностное натяжение. Вандерваальсовые силы притяжения, действующие между молекулами поверхностного слоя, обычно называют силами поверхностного натяжения. У разных жидкостей они разные. Их величина характеризуется коэффициентом поверхностного натяжения s. Уясним его смысл.
 Если на поверхности жидкости мысленно выделить произвольный контур, то молекулы, лежащие по одну сторону линии контура, притягиваются к молекулам, лежащим по другую сторону (рис.56). Поскольку жидкость изотропна, то сила поверхностного натяжения, приходящаяся на определенный отрезок длины контура, не зависит от его ориентации. Величина этой силы, приходящаяся на единицу длины контура, равна численно коэффициенту поверхностного натяжения s. Единица s - Н|м.
Если на поверхности жидкости мысленно выделить произвольный контур, то молекулы, лежащие по одну сторону линии контура, притягиваются к молекулам, лежащим по другую сторону (рис.56). Поскольку жидкость изотропна, то сила поверхностного натяжения, приходящаяся на определенный отрезок длины контура, не зависит от его ориентации. Величина этой силы, приходящаяся на единицу длины контура, равна численно коэффициенту поверхностного натяжения s. Единица s - Н|м.
 Найдем работу по увеличению площади поверхности пленки.
Найдем работу по увеличению площади поверхности пленки.
Пусть в рамке шириной a, на которой натянута жидкая пленка (рис.57), очень медленно перемещается перекладина под действием силы F = 2as на расстояние dl (2a потому, что у пленки две поверхности). Работа внешних сил перемещения перекладины идет на увеличение поверхностной энергии жидкости.
dA = dEп = Fdl = 2as×dl = sdS. (17.1)
Здесь dS = 2a×dl – приращение площади поверхности жидкости.
Отсюда Eп 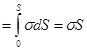 . (17.2)
. (17.2)
Итак, коэффициент s можно определить двумя способами.
а. 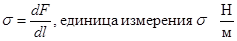 . Это сила поверхностного натяжения, отнесенная к единице длины контура.
. Это сила поверхностного натяжения, отнесенная к единице длины контура.
б. 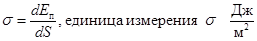 . Это энергия поверхностного слоя, отнесенная к единичной площадке.
. Это энергия поверхностного слоя, отнесенная к единичной площадке.
| Опытные значения s для разных веществ Таблица 17 | |||||||
| Вещество | Пограничная среда | T, K | s, Н/м | Вещество | Пограничная среда | T, K | s, Н/м |
| Олово Ртуть Ртуть Висмут | Углекислый газ Пары ртути Воздух Углекислый газ | 0,526 0,487 0,481 0,346 | Вода Масло каст. Скипидар Эфир этил. | Воздух Воздух Воздух Пары собств. | 0,073 0,033 0,027 0,016 |
3. Взаимодействие жидкости с другими телами. Поскольку молекулы поверхностного слоя жидкости взаимодействуют не только между собой, но и с молекулами контактирующей с жидкостью среды, то свойства этой среды неизбежно влияют на величину поверхностного натяжения жидкости.
а. Взаимодействие жидкостей с газами очень слабое. Состав газов над жидкостью мало влияет на величину s. Опыты показывают, что величина s для данной жидкости максимальна на границе жидкость – собственный пар (Таблица 18).
| Поверхностное натяжение на границе с газами и жидкостямиТаблица 18 | |||||||
| Вещество | Пограничная среда | T, K | s, Н/м | Вещество | Пограничная среда | T, K | s, Н/м |
| Ртуть Hg Ртуть Hg Ртуть Hg Ртуть Hg | Пары Hg Воздух Вода жидк. Спирт жидк. | 0,490 0,472 0,427 0,399 | Вода H2O Вода H2O Вода H2O Вода H2O | Пары H2O Воздух Бензол жидк. Эфир жидк. | 0,073 0,073 0,034 0,012 |

| |
|
Рассмотрим каплю какой-либо жидкости, помещенную на поверхность другой жидкости (рис.58).
Полагаем каплю настолько малой, чтобы массовыми силами можно было пренебречь.
 Здесь
Здесь 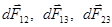 – силы поверхностного натяжения, действующие на элемент длины dl границы раздела 3-х сред.
– силы поверхностного натяжения, действующие на элемент длины dl границы раздела 3-х сред.
Когда капля примет окончательную форму и будет находиться в равновесии, сумма сил обратится в нуль (рис.59).
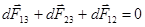 . Так как dF13 = s13dl, dF23 = s23dl, dF12 = s12dl, то, представив dF13 по теореме косинусов и разделив все члены на dl, получаем:
. Так как dF13 = s13dl, dF23 = s23dl, dF12 = s12dl, то, представив dF13 по теореме косинусов и разделив все члены на dl, получаем:
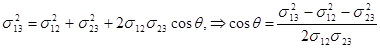 . (17.3)
. (17.3)
Если q ® 0, капля растекается в мономолекулярный слой. В остальных случаях капля растекается до некоторого максимального диаметра и переходит в устойчивое состояние.
Углы q1 и q2, образуемые касательными к поверхностям контактирующих сред, проведенными из границы раздела 3-х сред, называются краевыми углами. Когда q ® 0, говорят о полном смачивании одной жидкостью другой. Например, бензин и вода.
в. Взаимодействие жидкостей с твердыми телами. Если малая капля жидкости находится на плоской поверхности твердого тела (рис.60), то ее равновесию соответствует равенство: 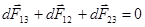 . Спроектировав уравнение на ось x, совпадающую с поверхностью твердого тела, и разделив его на dl, получаем выражение для краевого угла:
. Спроектировав уравнение на ось x, совпадающую с поверхностью твердого тела, и разделив его на dl, получаем выражение для краевого угла: 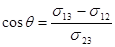 . (17.4)
. (17.4)
 В зависимости от величины q различают:
В зависимости от величины q различают:
При q = 0 – полное смачивание (керосин по стали),

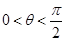 – частичное смачивание (рис.61-а),
– частичное смачивание (рис.61-а),
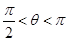 –частичное несмачивание (парафин-вода рис.61-б),
–частичное несмачивание (парафин-вода рис.61-б),
q = p – полное несмачивание (ртуть-стекло).
Взаимодействие молекул жидкости с молекулами твердого тела влияет на форму поверхности жидкости, налитой в сосуд. В результате образуется мениск - поверхность 2-го порядка. Если сосуд широкий, то поверхностные силы уступают массовым, и поверхность мениска совпадает с эквипотенциальной поверхностью силового поля. Если же размеры сосуда малы (@1 мм), то преобладают поверхностные силы. В этом случае мениск имеет самостоятельную кривизну.
4. Зависимость поверхностного натяжения от температуры. С повышением температуры жидкость разрыхляется, расстояние между молекулами увеличивается, а силы притяжения между ними уменьшаются.
С другой стороны, с ростом температуры увеличивается плотность насыщенных паров жидкости, силы притяжения, действующие на молекулы жидкости со стороны молекул пара, увеличиваются.
Оба эти механизма должны приводить к уменьшению поверхностного натяжения с ростом температуры. В критической точке, когда исчезает разница между жидким и газообразным состояниями, коэффициент поверхностного натяжения должен обращаться в нуль.
 Общий вид зависимости s(T) можно найти из термодинамических соображений. Воспользуемся для мысленного эксперимента рамкой с подвижной перекладиной, на которой натянута жидкая пленка (рис.57).
Общий вид зависимости s(T) можно найти из термодинамических соображений. Воспользуемся для мысленного эксперимента рамкой с подвижной перекладиной, на которой натянута жидкая пленка (рис.57).
Проведем цикл Карно, растягивая и сжимая пленку. Пусть в состоянии 1 пленка имеет площадь S1 при температуре T. В системе координат s, S этому состоянию соответствует точка 1 (рис.62).
а. Изотермически растянем пленку из состояния 1 в состояние 2, ее площадь увеличится от S1 до S2. Поверхностная энергия при этом также увеличится. Чтобы температура пленки осталась постоянной, к ней надо подвести тепло Q1. Работа расширения A1®2 = s (S2 - S1).
б. Адиабатически растянем пленку из состояния 2 в состояние 3 на бесконечно малую величину площади dS. Температура пленки понизится от T до T - dT, а поверхностное натяжение станет больше на величину ds.
в. Изотермически сожмем пленку, дав возможность ей сократиться при температуре T - dT (переход 3 ® 4). Площадь уменьшится на величину DS = S2 - S1. Для поддержания температуры пленки постоянной, от нее надо отвести тепло Q2.
г. Адиабатически сожмем пленку, дав возможность ей сократиться без притока тепла на величину dS. Температура при этом повысится на величину dT, а поверхностное натяжение уменьшится на величину ds (переход 4 ® 1). Цикл завершен.
Работа этого обратного цикла отрицательна и равна площади бесконечно тонкой трапеции 1 ® 2 ® 3 ® 4. dA = – ds (S2 - S1). От внешних тел получено тепло Q1 - Q2.
КПД цикла 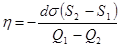 . (17.5)
. (17.5)
Так как цикл идеальный, то по теореме Карно: 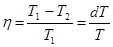 . (17.6)
. (17.6)
Отсюда 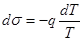 . (17.7)
. (17.7)
Коэффициент q = (Q1 - Q2)| (S2 - S1) есть количество тепла, которое надо подвести к единице площади пленки при совершении цикла. Поскольку пленка совершает обратный цикл, то это тепло в данном случае должно отводиться от пленки.
В общем случае q зависит от температуры и с ростом T несколько уменьшается. Однако во многих случаях величину q можно считать постоянной, что упрощает интегрирование уравнения (17.7). s = – qlnT + lnC. (17.8)
Если постоянную интегрирования lnC найти из условия, что поверхностное натяжение в критической точке исчезает, 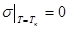 , то lnC = qlnTк, и
, то lnC = qlnTк, и
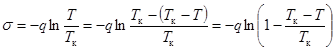 . (17.9)
. (17.9)
Поскольку T всегда меньше Tк, то выражение (Tк- T) | Tк< 1. Это позволяет разложить логарифм в ряд и ограничиться первым членом, ln(1+x)|x<1= x. 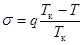 . (17.10)
. (17.10)
На практике коэффициент q определяют, измерив s при некоторой определенной температуре. Удобно взять для этого точку замерзания-плавления Tпл.
Тогда 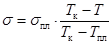 . (17.11)
. (17.11)
Здесь sпл – поверхностное натяжение в точке замерзания жидкости.
Дата добавления: 2020-05-20; просмотров: 1627;











