Распределение молекул газа по скоростям. Функция распределения Максвелла

1. Функция распределения.Благодаря тому, что молекулы реальных газов имеют конечный объем и потому часто сталкиваются друг с другом, их скорости изменяются. Но оказывается, что в любой момент времени распределение молекул по скоростям, как показывают теория и опыт, вполне определённое и единственно возможное.

Задачу о распределении молекул по скоростям можно сформулировать так: какая часть молекул обладает скоростями, лежащими в некотором интервале вблизи заданной скорости.

Рассмотрим газ в некотором объеме, в котором отсутствуют силовые поля. Пусть n – концентрация молекул, то есть число молекул в единице объема, а dn/n – доля тех молекул, скорости которых лежат в интервале значений от u до u + du, где du – ширина интервала скоростей. Очевидно, что чем шире интервал du, тем больше доля молекул, чьи скорости в нем заключены, dn/n ~ du. (9.1)

Можно предположить, что коэффициент пропорциональности между этими величинами для разных скоростей разный и является функцией скорости u. Тогда соотношение (9.1) переходит в равенство. dn/n =f(u)du. (9.2)

Функцию f(u) называют функцией распределения. Ее нашел теоретически Джеймс Максвелл в 1859 г. 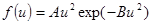. Функция распределения, Дж. Максвелл, 1859 (9.3)

Здесь B = m|2kT, A = 4p(m|2pkT)^{3| 2}= 4p(B|p)^{3| 2}, где m – масса каждой молекулы, T – абсолютная температура газа, k – постоянная Больцмана. Функция получена методами теории вероятностей на основе гипотезы о равновероятности всех направлений скоростей молекул. (Подробнее см., например, в кн. [1] глава 6, с.с.234-235).

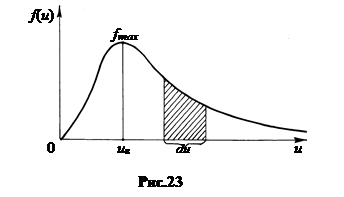2. График функции распределения представляет собой колоколообразную несимметричную кривую с одним максимумом (рис.23). Левый конец кривой находится в центре системы координат f, u.

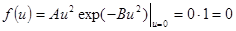. (9.4)

При u → ∞ lim f(u) = 0, так как скорость убывания экспоненты 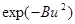преобладает над скоростью возрастания степенной функции u².

Коэффициент A в функции распределения (9.3) подобран так, чтобы интеграл от f(u) в пределах от 0 до + ∞ равнялся 1. Говорят, функция f(u) нормирована на единицу. На графике единице равняется площадь под кривой. Относительная доля молекул dn/n, чьи скорости заключены в интервале от u до u + du, определяется на графике площадью заштрихованного столбца. В конечном интервале скоростей она всегда меньше 1.

Применительно к одной молекуле функция f(u) называется плотностью вероятности. Площадь столбца f(u)×du определяет в этом случае вероятность того, что скорость молекулы окажется в данном интервале скоростей. Тождественность между функцией плотности вероятности для одной молекулы и функцией распределения для ансамбля молекул справедлива лишь для систем с огромным числом частиц.

Из поведения функции распределения f(u) в правой части графика следует, что формально в любой газовой системе всегда существует отличная от нуля вероятность того, что в газе найдутся молекулы со сколь угодно большими скоростями.

На самом деле это не так. Принципиальным ограничением здесь является то, что энергия одной молекулы не может быть больше внутренней энергии всего газа в целом. Если принять во внимание, что в реальных газах молекулы не бесструктурные упругие шарики, а агрегаты, способные разрушаться, то ограничения наступают еще раньше.

В одноатомных газах максимальная реальная скорость ограничена температурой ионизации, при которой соударения перестают быть абсолютно упругими. Эту максимальную скорость можно оценить из формулы среднеквадратичной скорости (7.13). Приняв в качестве Т_иониз = 10⁴ К, получаем для гелия .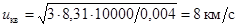

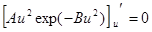3. Наиболее вероятная скоростьu_в – это скорость, на которую приходится максимум функции распределения f(u). Чтобы найти ее, надо исследовать функцию f(u) на экстремум. f ¢(u) = 0, или . (9.5)

Дифференцируем.

.

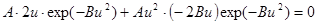Так как 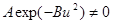, то 1 - Bu² = 0.

Отсюда 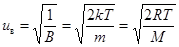. (9.6)

Вероятность того, что скорость молекулы окажется в интервале, включающем u_в, больше вероятности относительно любой другой скорости при той же ширине интервала.

Наибольшая часть молекул газа имеет скорости, лежащие вблизи значения u_в. Для азота при температуре T = 273 K u_в = 402 м/с, для водорода u_в = 1506 м/с, для хлора u_в = 253 м/с.

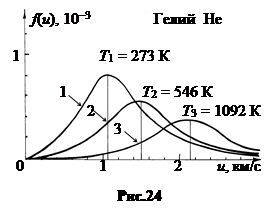
С повышением температуры газа скорость u_в увеличивается. На рис.24 показаны графики функции распределения f(u) при температурах T₁ = 273 K (кривая 1), T₂ = 2T₁ = 546 K (кривая 2), T₃ = 4T₁ = 1092 K для гелия.

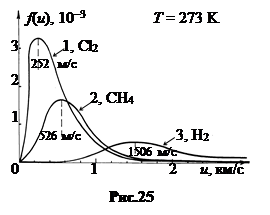
С ростом молярной массы скорость u_в уменьшается. На рис.25 показаны кривые распределения для хлора Cl₂ (M = 0,071 кг/моль, кривая 1), метана СH₄ (M = 0,016 кг/моль, кривая 2) и водорода H₂ ( 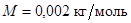, кривая 3) при T = 293 K.

Максвелловское распределение молекул по скоростям является равновесным. Каково бы ни было распределение в начальный момент времени, оно все равно в конечном счете перейдет в максвелловское f(u). Это доказал Больцман в 1871 г.

4. Средняя квадратичная скорость u_кв. Знание функции распределения f(u) позволяет вычислить любую из средних скоростей. В качестве критерия верности функции распределения f(u) представляет интерес вычисление среднеквадратичной скорости, поскольку выражение для нее получил двумя годами раньше Р.Клаузиус при выводе основного уравнения кинетической теории газов (см. §7).

По определению, 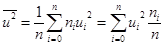. (9.7)

При очень больших n, а именно такова концентрация молекул в газах, сумма переходит в интеграл. 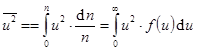. (9.8)

Подставим f(u). 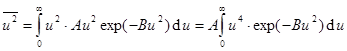. (9.9)

Интеграл вида 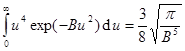(9.10)

называется 5-м интегралом Пуассона. (Вычисление этих интегралов показано в кн.: Радушкевич Л.В. Курс статистической физики. Учебное пособие. – М.: Просвещение 1966. с.410). Тогда, подставив выражения интеграла и коэффициента A, получаем

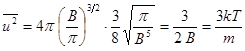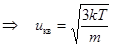, . (9.11)

Формула среднеквадратичной скорости (9.11), полученная на основе функции распределения Максвелла, совпадает с формулой (7.13), полученной Клаузиусом.

5. Средняя арифметическая скорость (средняя по модулю) 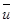вычисляется аналогично. 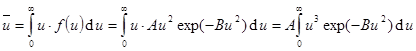. (9.12)

Интеграл вида 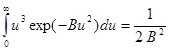(9.13)

называется 4-м интегралом Пуассона (См. в кн. Л.В. Радушкевича). Подставляем.

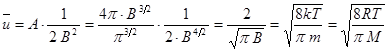. (9.14)

Из отношения скоростей видно, что самая большая - u_кв самая маленькая - u_в.

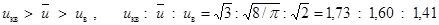=1,22 : 1,13 : 1.

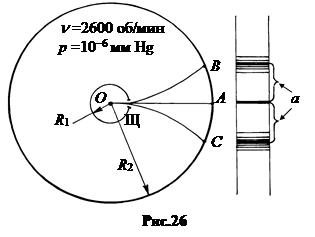6. Опыты Штерна.Прямой проверочный эксперимент поставил впервые Отто Штерн в 1920 г. с помощью атомных пучков. Схема установки показана на рис.26.

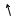Два коаксиальных жестко связанных между собой цилиндра радиусами R₁ и R₂ вращались с угловой скоростью ω сначала в одну сторону, затем в другую. Платиновая нить, покрытая серебром и натянутая вдоль геометрической оси цилиндров, нагревалась до температуры около 1300 K. При этом серебро испарялось. (T_пл серебра 1235 К). Часть испарившихся атомов серебра, пройдя через щель Щ, формировали узкий пучок. Скорость u движения атомов в этом пучке находилась так.

За время движения атомов между цилиндрами t = (R₂ - R₁)/u цилиндры поворачиваются на угол j=wt = w(R₂ - R₁)/u. Атомный осадок на внутренней стенке большого цилиндра смещается относительно центральной проекции щели (точка А) в точки B или C на расстояние a = R₂j= wR₂(R₂ - R₁)/u. Отсюда находится скорость движения атомов в пучке. 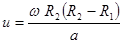. (9.15)

Штерн получил из опытов u » 600 м/с для атомов серебра при температуре нити 1300 К. Это качественно согласуется с распределением Максвелла. Наиболее вероятная скорость для атомов серебра 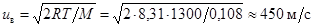, среднеквадратичная скорость u_кв » 550 м/с. Если учесть, что расстояние a до центра пятна на внутренней поверхности большого цилиндра находилось по визуальной плотности осадка, это неплохое соответствие теории эксперименту.

Сравнение осадка в точке A, полученного при покоящихся цилиндрах, с осадками в точках B и C показало, что если края полосы в точке A резко очерчены, а осадок в пределах полосы однородный, то края полос B и C размыты, плотность осадка убывает от середины к краям. Это говорит о том, что скорости атомов в пучке разные.

Недостаток первых опытов Штерна состоял в том, что атомы серебра выходили не из газа, а с поверхности твердого тела. Поэтому они несли информацию о распределении скоростей не в газе, а в твердом теле.

В 1947 г. опыты были повторены с парами цезия. Атомы цезия шли в пучок из паров над тиглем после многократных взаимных столкновений. Поэтому они несли информацию о распределении скоростей молекул в газовой системе. Опыты также подтвердили распределение Максвелла.

В период с 1920 по 1960-е годы были выполнены эксперименты другими исследователями с атомами кадмия, ртути, калия, таллия, висмута, а также с термоэлектронами. Все они показали очень хорошее соответствие теории Максвелла опыту.

7. Безразмерная скорость.В физике широко используется прием перехода в уравнениях и формулах к безразмерным параметрам. Для этого выбирается какая-то характерная величина с той же размерностью, и через нее выражается размерный параметр. В распределения Максвелла это наиболее вероятная скорость u_в.

Обозначим скорость движения молекул u = сu_в, где с = u/u_в - безразмерная скорость. После подстановки в формулу (9.2) выражени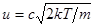й и 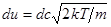получаем универсальную для всех газов при любой температуре функцию распределения, выраженную через безразмерную скорость.

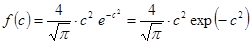. (9.16)

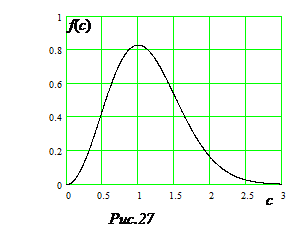
Максимум функции f(c) соответствует скорости c = 1 (рис.27).

8. Универсальность распределения Максвелла.Функция распределения Максвелла не зависит от характера взаимодействия частиц системы и от внешних сил. Поэтому она справедлива как для молекул газа, так и для молекул жидкости и твердых тел. Справедлива она также для броуновских частиц, взвешенных в газах и жидкостях.

Распределение Максвелла справедливо не только для мгновенных скоростей многих молекул газа, но и для последовательности скоростей одной молекулы в течение некоторого времени τ.

Минимальное время τ можно оценить, исходя из минимального объема газа. Если принять, что в объеме 1 мм³ газ при нормальных условиях сохраняет еще все свойства газа, то такой системе с N числом частиц можно поставить в соответствие 1 частицу, испытавшую N соударений. Так как время одного соударения t₀ » 10^-10 c, то t =Nt₀= 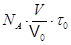. (9.17)

Здесь V = 1 мм³ - взятый для оценки объем, V₀ = 22,4×10^-3 м³|моль – молярный объем газа при нормальных условиях. .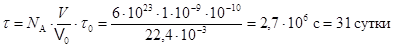

За это время значения скоростей молекулы равномерно заполняют все пространство под кривой распределения.

§10. Газ в поле силы тяжести. Распределение Больцмана. Газовые
оболочки небесных тел

1. Атмосферы планет.Если бы не было теплового движения молекул, то под действием силы тяжести все молекулы газа собрались бы на поверхности планеты. А если бы не было силы тяжести, то все молекулы газа разлетелись бы в мировое пространство. Таким образом газовые оболочки планет существуют благодаря хаотическому движению молекул и силе тяжести.

2. Барометрическая формула для центрально-симметричного поля тяготения.Найдем зависимость давления газа в атмосфере планеты от расстояния до центра в пространстве над поверхностью планеты (рис.28).

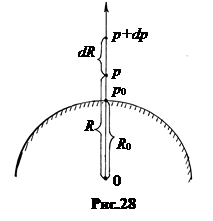Пусть на поверхности планеты радиуса R₀ давление газа p₀. С ростом высоты давление убывает. Поэтому приращение давления отрицательно, dp = - rgdR. (10.1)

Но 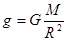– ускорение силы тяжести. Здесь M – масса планеты, G – гравитационная постоянная. Плотность газа ρ зависит от давления. Так как r = n×m, где m – масса отдельной молекулы, то выразив концентрацию n из уравнения Клаузиуса p = nkT, n = p/kT, получаем.

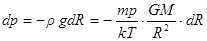. (10.2)

Это дифференциальное уравнение 1-го порядка. Разделим переменные p, R и проинтегрируем.

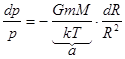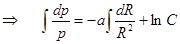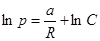, , . (10.3)

Постоянную C найдем из краевого условия:

. , .

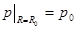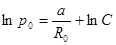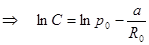Подставляем. 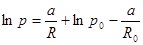, или 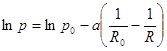. (10.4)

Потенцируем и возвращаемся к исходным величинам.

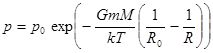. Барометрическая формула. (10.5)

Это барометрическая формула для центрально-симметричного поля тяготения для пространства R ≥ R₀.

3. Барометрическая формула для однородного поля тяготения.У многих планет газовая оболочка очень тонкая. У Земли, например, она не более 4-5% радиуса. Поэтому при малых перепадах высот изменением напряженности поля тяготения можно пренебречь и считать его постоянным. Формула в этом случае упрощается.

Обозначим R = R₀ + h, где h<<R₀. Тогда

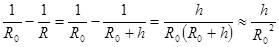и 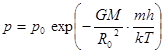. (10.6)

Здесь 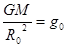- ускорение силы тяжести на поверхности планеты. Þ .

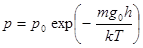Барометрическая формула для однородного поля тяготения (10.7)

4. Распределение Больцмана.Если в барометрической формуле (10.7) перейти от давления к концентрации по формуле Клаузиуса p = nkT, то получаем закон распределения молекул газа по высоте в однородном поле силы тяжести.

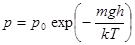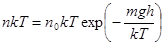, или , или 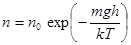. (10.8)

В показатель экспоненты входит потенциальная энергия молекул в поле силы тяжести

П = mgh. Так что 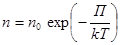. Распределение Больцмана, 1866. (10.9)

Распределение молекул или каких-то других частиц в потенциальном силовом поле в условиях теплового равновесия по величине потенциальной энергии называется распределением Больцмана. Физическая природа силового поля роли не играет. Важно лишь, чтобы поле было постоянно и консервативно. Поэтому распределение вида (10.9) применимо и к другим объектам природы, например, к электронам проводимости в металлах.

5. Опытная проверка барометрической формулы.Как следует из формул (10.7) и (10.8), давление и концентрация частиц в газовой оболочке уменьшаются с высотой тем быстрее, чем больше масса молекул газа. Скорость изменения p и n удобно характеризовать толщиной слоя h, в котором давление и концентрация частиц изменяются в e = 2,7 раз. В этом случае 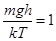, 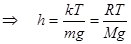. (10.10)

В водородной атмосфере Земли при T = 273 K величина h около 120 км, в азотной – 8,3 км, в атмосфере углекислого газа (СО₂, М = 44×10^-3 кг/моль) h = 5,2 км.

Опытную проверку барометрической формулы удобно делать на эмульсиях, дымах или туманах. Так, например, масса капельки воды диаметром 0,1 мкм составляет 5×1^-19 кг. В 1908-1909 г. Жан Перрен показал, что такие взвешенные броуновские частицы можно трактовать как невзаимодействующие между собой молекулы очень больших размеров. Толщина слоя тумана из таких капелек, в котором концентрация частиц изменяется в e раз, составляет около 0,75 мм. Это позволяет измерять концентрацию частиц визуально с помощью оптического микроскопа.

Перрен работал с эмульсиями, которые он получал, растворяя смолу мастикового дерева в спирте, а затем разбавляя спиртовый раствор водой. Размер шариков достигал здесь 1 мкм. Размер шариков эмульсии, полученной аналогичным образом из сока гевеи, составлял 0,4 мкм. Эмульсия помещалась в герметичную горизонтальную кювету высотой 0,1 мм, и с помощью вертикального тубуса подсчитывалась концентрация частиц на разных высотах.

Перрен показал, что равновесное распределение концентрации по высоте устанавливается уже через 1 час, после приготовления эмульсии и соответствует формуле Больцмана.

6. Неравновесность газовых оболочек.Из формулы (10.5) следует важный вывод. При R ® ∞ давление и концентрация молекул газа не обращаются в нуль.

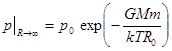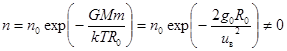, (10.11)

Здесь 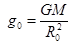, 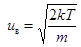– наиболее вероятная скорость молекул газа. Для азота при Т = 273 К u_в = 4×10² м/с. Остаточная концентрация молекул азотной атмосферы, например, Земли, составляет 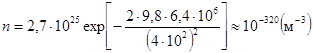. (10.12)

И хотя это исчезающе малая величина, формально-логический подход приводит к заключению, что в бесконечном пространстве равновесная атмосфера должна иметь бесконечную массу. Но физически это невозможно.

Следовательно, газовые оболочки планет (и звезд) неравновесны. Газ непрерывно растекается в мировое пространство. Причем уходят молекулы, скорость которых достигает второй космической. Эти быстрые молекулы находятся в правой части распределения Максвелла. В результате средняя энергия оставшихся молекул уменьшается, температура газа понижается. Из смеси газов в первую очередь уходят самые легкие – водород и гелий. Поэтому в атмосфере Земли, например, этих газов практически нет.

Чем меньше масса планеты, тем меньше для нее 2-я космическая скорость, тем быстрее планета теряет свою газовую оболочку. Поэтому на Луне и Меркурии, например, нет признаков атмосфер. С повышением температуры газа время рассеивания атмосферы уменьшается.

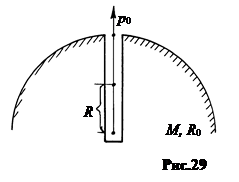7. Барометрическая формула для пространства внутри планет.Вопрос: как изменяется давление и концентрация частиц газа в пространстве ниже поверхности планеты вполне актуален, поскольку существуют такие объекты как Юпитер с его мощной газовой оболочкой и космические газовые шары – звезды на разных стадиях их развития. Решение задачи усложняется тем, что становится неопределенным характер распределения плотности вещества с глубиной, вид зависимости напряженности гравитационного поля и др. Поэтому ограничимся простым случаем распределения газового давления в радиальной шахте однородной планеты (рис.29).

Характер изменения ускорения силы тяжести g в однородном шаре радиуса R₀ нашел Ньютон в своей первой задаче тяготения, g = g₀RçR₀, где g₀ – ускорение свободного падения на поверхности шара.

Рассмотрим два случая: а) газ неограниченно сжимаем, б) газ сжимаем ограниченно.

а. Газ сжимаем неограниченно.Перепишем уравнение (10.1).

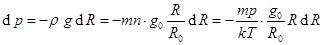или 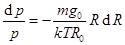(10.13)

После интегрирования при начальном условии p = р₀при R = R₀ получаем:

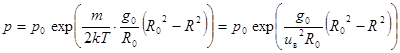. (10.14)

Для неограниченно сжимаемого газа с М = 29×10^-3 кг/моль при Т = 273 К в центре шара давление максимально. .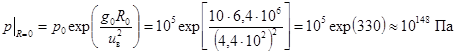

Плотность вещества при таком давлении колоссальна и много больше плотности ядер.

Этот далекий от здравости смысла результат получился потому, что газ полагался идеальным, состоящим из материальных точек и способным сжиматься неограниченно. В реальных же газах сжимаемость резко уменьшается, когда расстояние между центрами молекул приближается к одному диаметру молекул.

б. Ограниченно сжимаемый газ.Предположим, что газ вначале сжимается, но когда его плотность сравняется с плотностью жидкости, он ведет себя как несжимаемая жидкость. В обычных условиях плотность газа примерно на 3 порядка меньше плотности жидкости (плотность азота при нормальных условиях 1,25 кг/м³, а плотность жидкого азота около 860 кг/м³). Так как отношение плотностей равно отношению концентраций частиц, то радиус сферы R_ж, на котором плотность газа сравняется с плотностью жидкости, найдется из условия: 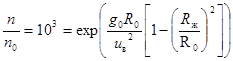, 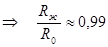(для Земли).

По сравнению с радиусом планеты это небольшая глубина. Для Земли она составляет всего около 63 км. Приращение давления с радиусом R на глубинах постоянной плотности R ≤ R_ж принимает вид: 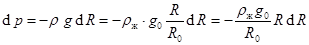. (10.15)

При краевом условии 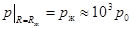получаем: 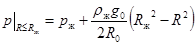(10.16)

При R << R_ж можно полагать R_ж = R₀, так что получаем: 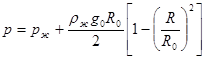. (10.17)

Для Земли при р_ж = 10³р₀ и r_ж = 10³ кг/м³ в центре планеты (R = 0) p » 10¹⁰ Па.