Квадратичные неравенства и области

Неравенства, содержащие квадратичные выражения, могут быть решены методом разложения на множители или же методом дополнения до полного квадрата.

Например, х² - 2х - 3 разлагается на множители в виде (х + 1)(х - 3); выражение бх² + 1х - 5 разлагается на множители как (2х - 1)(3х + 5).

Если квадратичное выражение не разлагается на множители, то используется метод дополнения до полного квадрата. Для выражения типа х² + bх + с данная процедура в общем виде такова:

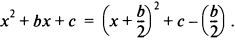
Например, x²+ 4х - 7 не разлагается на множители, а дополнение до полного квадрата дает

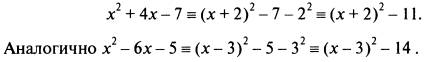
Пример. Решить неравенство х² + 2х - 3 > 0.

Разлагаем х² + 2х – 3 > 0 на множители: (x - 1)(x + 3).

Произведение (x - 1)(x + 3) положительно, если a) (x - 1) > 0 и (x + 3) > 0, б) (x - 1) < 0 и (x + 3) < 0.

а) Поскольку (x - 1) > 0, тo x > 1, и поскольку (х + 3) > 0, тo х > -3.
Оба этих неравенства верны одновременно только при х > 1.

б) Поскольку (х - 1) < 0, тo х < 1, и поскольку (х + 3) < 0, то х < -3.

Оба этих неравенства верны одновременно только при х < -3. Итак, неравенство х² + 2х - 3 > 0 верно только при х > 1 или x < -3.

Пример. Решить неравенство у² - 8у - 10 ≥ 0.

Выражение у² - 8у - 10 на множители не разлагается. Применим метод дополнения до полного квадрата:

у² - 8у - 10 ≡ (у - 4)² – 10 - 4² ≡ (у-4)² – 26.

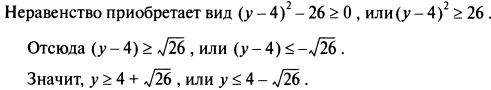
Следовательно, у² - 8у - 10 ≥ 0 верно при у ≥ 9.10 или у ≤ -1.10 с точностью до двух знаков после десятичной точки.

Области. Область — это множество точек на координатной плоскости, удовлетворяющих некоторому неравенству.

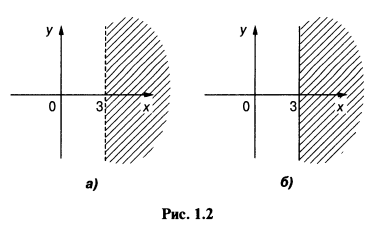
Например, на рис. 1.2а заштрихованная область задается неравенством х > 3, прямая х = 3 показана пунктиром, а на рис. 1.2б заштрихованная область определяется неравенством х ≥ 3, прямая х = 3 показана сплошной линией. Область х ≥ 3 включает все точки на прямой х = 3 и справа от нее.

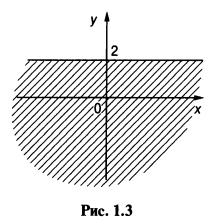
Аналогично заштрихованная область на рис. 1.3 определяется неравенством у ≤ -2.

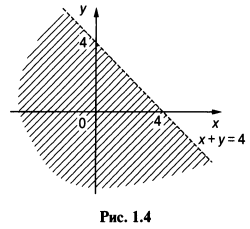
На рис. 1.4 пунктиром показана прямая х + у = 4 (отметим, что если х + у = 4, то у = -х + 4, а это прямая линия с тангенсом угла наклона -1, пересекающая ось у в точке у = 4); заштрихованная область определяется как х + у < 4.

Пример. Показать на декартовой плоскости следующие области: а) у > 3х - 2, б) х + 2у < 8.

а) На рис. 1.5 показана прямая у = 3х - 2, а заштрихованная область определяется неравенством у > 3х - 2.

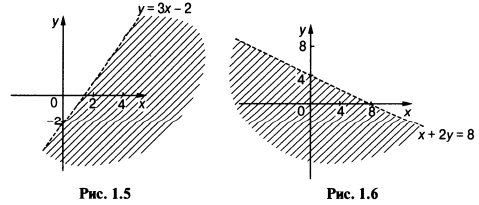
б) На рис. 1.6 пунктиром показана прямая х + 2у = 8 (т. е. 2у = -х + 8 или у = -1/2х + 4 , это прямая с тангенсом угла наклона -1/2 , пересекающая ось у в точке у = 4), и заштрихованная область определяется неравенством х + 2у < 8. (Для проверки возьмем любую точку, например х = 1, у = 1, тогда х + 2у = 1 + 2 = 3, это меньше 8. Заштрихованная область включает все точки, для которых х + 2у < 8.).