Арифметические и геометрические прогрессии

Если для последовательности характерна постоянная величина разности между соседними членами, она называется арифметической прогрессией. Примеры арифметической прогрессии:

1. 1, 4, 7, 10, 13,..., где разность (модуль) арифметической прогрессии равна 3;

2. а, а + d, а + 2d, а + 3d,..., где разность арифметической прогрессии равна d.

Если первый член арифметической прогрессии а, и модуль прогрессии d, тогда n-й член дается выражением

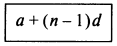
В первом примере седьмой член определяется как 1 + (7 - 1)3 = 19, что можно легко проверить.

Сумма арифметической прогрессии S может быть получена при умножении среднего арифметического всех членов на количество членов.

Среднее всех членов есть a + l/2 , где а - первый член, а l — последний член, т. е. l = а + (n - 1)d для n членов.

Тогда сумма n членов

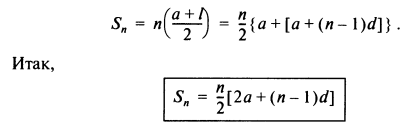
Пример. Сумма первых 7 членов ряда 1, 4, 7, 10, 13,... (где а = 1 и d = 3) определяется как

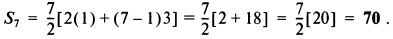
Пример. Определить: а) девятый и б) шестнадцатый члены последовательности 2, 7, 12, 17,....
2, 7, 12, 17,... — арифметическая прогрессия с модулем d = 5.

а) n-й член арифметической прогрессии определяется как а + (n - 1 )d.

Первый член а = 2, d = 5 и n = 9, тогда девятый член равен 2 + (9 - 1)5 = 2 + (8)(5) = 2 + 40 = 42.

б) 16-й член - это 2 + (16 - 1)5 = 2 + (15)(5) = 2 + 75 = 77.

Геометрические прогрессии. Если между соседними членами последовательности существует постоянное отношение, она называется геометрической прогрессией. Постоянное отношение называется знаменателем геометрической прогрессии, г.

Примеры геометрической прогрессии:

1, 2, 4, 8,где знаменатель равен 2;

a₁, a₁r, a₁r², a₁r³,... где знаменатель равен r. Тогда n-й член b_n определяется формулой

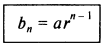
что может быть легко проверено с помощью приведенных выше примеров.

Например, восьмой член геометрической прогрессии 1, 2, 4, 8... — это 1 ∙2⁷ = 128, поскольку a = 1 и r = 2.

Сумма n членов

Пример. Сумма первых восьми членов геометрической прогрессии 1, 2, 4, 8,16,... (где а = 1 и r = 2) определяется формулой

Пример. Фирма, дающая напрокат инструменты, обнаружила, что ее чистая прибыль за год от проката определенного инструмента ежегодно уменьшается на 10%. Чистый доход с определенного инструмента в этом году составил 400 фунтов. Определим всю возможную прибыль от проката этого инструмента в будущем (предполагаем, что инструмент вечен).

Чистая прибыль образует следующую последовательность: 400 фунтов + 400 фунтов х 0.9 + 400 фунтов х 0.9² + ..., которая является геометрической прогрессией с а = 400 и r = 0.9.

Сумма бесконечной геометрической прогрессии

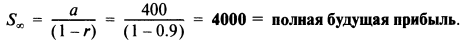
Пример. Сверлильный станок должен иметь диапазон скоростей от 50 до 750 оборотов в минуту. Определим значения скоростей, каждую с точностью до ближайшего целого числа, при условии, что скорости образуют геометрическую прогрессию.

Следовательно, шесть скоростей сверлильного станка суть 50, 86, 148, 254, 436 и 750 оборотов в минуту с точностью до ближайшего целого числа.