Выражения, уравнения и тождества

Примером алгебраического выражения является, например, выражение (Зх - 5), а примером уравнения является, например, выражение Зх - 5 = 1, так как оно содержит знак равенства.

Уравнение в широком смысле — это просто утверждение равенства двух величин. Например, 1м = 1000 мм или F = 9/5С + 32 , или у = mх + с.

Различают два типа уравнений: собственно уравнения и тождества.

Тождество — отношение, которое верно для всех значений неизвестных переменных, в то время как собственно уравнение верно только при определенных значениях переменных. Например, Зх - 5 = 1 есть уравнение, поскольку оно верно только при х = 2, а Зх ≡ 8х - 5х есть тождество, поскольку оно верно для всех значений х (знак «≡» означает тождественно).

Простое линейное уравнение, или уравнение первой степени, — уравнение, в котором неизвестная величина имеет показатель степени 1.

Решить уравнение — значит найти неизвестную величину.

К уравнению может быть применено любое арифметическое действие, если при этом в уравнении сохраняется равенство.

Пример. Решить уравнение 4х = 20.

Делим каждую часть уравнения на 4 получаем 4x/4 = 20/4.

Заметим, что одна и та же математическая операция была применена и к левой (ЛЧ), и к правой (ПЧ) частям уравнения, так что равенство осталось в силе.

Пример. Решить уравнение 2x/5 = 6.

Чтобы избавиться от дроби, которая находится в левой части уравнения, умножаем обе части уравнения на 5. Получим

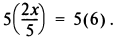
Сокращая, получаем 2х = 30. Затем делим обе части уравнения на 2 и получаем 2x/2 = 30/2 , откуда имеем х = 15.

Пример. Решить уравнение а - 5 = 8. Добавляя 5 к обеим частям уравнения, получаем

a - 5 + 5 = 8 + 5.

Следовательно, а = 13.

В результате выполненного действия число 5 переносится из левой части уравнения в правую, и при этом знак при числе 5 меняется на противоположный, т. е. на +.

Пример. Решить уравнение 6х + 1 = 2х + 9.

В подобных уравнениях содержащие х члены группируют в одной из частей уравнения. Поскольку переносу из одной части уравнения в другую должна сопутствовать перемена знака, уравнение 6х + 1 = 2х + 9 принимает вид 6х - 2х = 9 - 1. Откуда 4х = 8 или 4x/4 = 8/4. Следовательно, х = 2.

Пример. Решить уравнение √x = 2 .

Уравнение √x = 2 — это не «простое уравнение», поскольку х имеет степень 1/2 , т. е. √x = х^1/2. Тем не менее этот пример заслуживает того, чтобы его здесь рассмотреть, поскольку часто встречается на практике.

Если неизвестная величина стоит под знаком квадратного корня, то обе части уравнения следует возвести в квадрат:

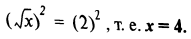
Пример. Решить уравнение х² = 25.

Уравнение содержит квадратичный член, и, значит, это не простое уравнение (в действительности это квадратное уравнение). Однако подобные уравнения приходится решать довольно часто, поэтому пример приводится здесь.

Если в уравнении содержится квадрат неизвестной величины, из обеих частей уравнения извлекают квадратный корень.

В результате получаем √x² = √25 . Следовательно, х = 5. Однако х = -5 тоже есть решение данного уравнения, поскольку (-5) х (-5) = +25.

Следовательно, при извлечении квадратного корня из числа всегда существует два ответа: один — положительный, второй — отрицательный.

Таким образом, решение для х² = 25 записывается в виде х = ±5.