ДВУХПАРАМЕТРИЧЕСКОЕ ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

При решении практических задач часто приходится оперировать со случайными величинами, минимальное значение которых ограничено некоторой постоянной величиной x=b. Такие величины применяются, например, для описания времени восстановления аппаратуры. Физически это означает, что во всех случаях для устранения неисправности требуется некоторое время .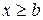

Плотность вероятности этого распределения имеет вид (так называемая сдвинутая экспонента)

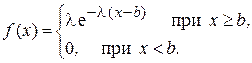
Математическое ожидание и дисперсия здесь равны

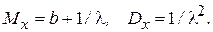
Рассмотрим, как получить на ЭВМ последовательность значений случайной величины с таким распределением.

Используем функциональное уравнение

.

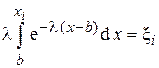После обычных преобразований получим рабочую формулу

.

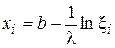Второе слагаемое в правой части формулы представляет собой случайную величину, подчиненную экспоненциальному распределению с параметром 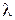. Следовательно, формирование случайной величины со сдвинутым экспоненциальным распределением сводится к получению (любым способом) экспоненциально распределенной случайной величины и суммированию ее с константой b.