Моделирование непрерывных распределений

Большинство методов моделирования случайных величин на ЭВМ с различными законами распределения основано на использовании следующей теоремы:

Если случайная величина x имеет плотность распределения f(x), то распределение случайной величины y=F(x) является равномерным на интервале (0,1).

Здесь под F(x) понимается интегральная функция распределения случайной величины x.

Следовательно, можно поступить наоборот: построить функцию распределения F(x); выбрать случайное значение y из равномерного распределения в интервале (0,1) и определить то значение аргумента х, для которого F(x)=y.

Полученная таким образом случайная величина x будет иметь заданную функцию распределения F(x).

Эта же задача может быть решена не только графическими построениями, но и рядом других способов. В частности, аналитический способ основан на обратном преобразовании x=F ^–1(y), где F ^–1 – функция, обратная F.

Это преобразование сводится к решению интегрального уравнения относительно x_i

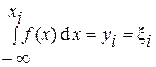, (1)

т.е. определяется такое значение x_i, при котором функция распределения равна y_i = ξ_i, где ξ_i – значение случайной величины, равномерно распределенной на интервале (0,1).

В общем случае применение аналитических способов решения этого уравнения связано со значительным расходом машинного времени. Однако в частных случаях, когда решение уравнения (1) можно получить в явном виде, этот способ очень удобен.

Одним из наиболее экономных (по затратам машинного времени) методов получения случайных чисел с заданным законом распределения является способ кусочной аппроксимации плотности распределения f(x).

Сущность этого метода состоит в том, что область возможных значений случайной величины х разбивается на n интервалов, количество которых определяется точностью аппроксимации плотности распределения f(x). Левую границу k–го интервала обозначим а_k.

Будем считать, что в пределах интервала (а_k, а_k+1), значение функции f_k(x) не изменяется, тем самым мы заменяем кривую f(x) ступенчатой функцией.

Если случайным образом из n интервалов выбрать интервал (а_k, а_k+1), то получение случайного числа х_i с плотностью f(x) сводится к формированию равномерного распределения в интервале (а_k, а_k+1)

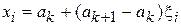. (2)

Для использования этой формулы необходимо располагать n значениями а_k, которые рассчитываются для заданного закона распределения f(x) и вводятся в оперативную память ЭВМ в порядке возрастания. Простейшая процедура расчета величин а_k основана на предположении, что вероятность попадания в любой из n интервалов одинакова и равна, очевидно, 1/n. Это означает, что мы выбираем такие интервалы, в которых приращение функции распределения F(x) при переходе от k–го к (k+1)–му интервалу было постоянным и равным 1/n, т.е.

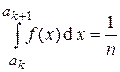. (3)

Вследствие нелинейности функции распределения F(x) (за исключением равномерного распределения) длина интервалов (а_k, а_k+1) получается различной.

Начальное значение а_k =а₀ всегда известно – оно равно минимальному значению случайной величины х. Следовательно, соотношение (3) позволяет последовательно вычислить все а_k (k = 1, …, n), т.е. решается оно относительно верхнего предела интегрирования. Значение n обычно принимается равным 2^m, где m=4…6 (n=16…64).

Для организации случайной выборки k–го интервала из равномерного распределения извлекается случайное целое число 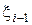и первые m разрядов используются в качестве адреса для выбора из таблицы значений а_k и а_{k +1}. Затем по формуле (2) определяется значение х_i, при этом используется уже новое случайное число .

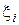Данный метод формирования случайных чисел находит широкое практическое применение благодаря своей универсальности и экономичности. Его недостатком является неравномерная точность аппроксимации.

Из рассмотрения методов моделирования случайных величин следует, что для их реализации необходимо иметь случайную величину ξ с равномерным распределением либо на интервале (0,1), либо на интервале (а_k,а_{k +1}), в общем случае на интервале (a, b).