МОДЕЛИРОВАНИЕ РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ

Случайная величина 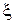, равномерно распределенная на интервале (0,1), имеет плотность распределения

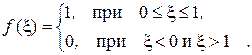
Ее математическое ожидание и дисперсия равны

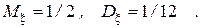
У ряда ЭВМ имеются специальные датчики случайных равномерно распределенных чисел, использующие либо физические принципы получения случайных чисел (например, шумы в электронных приборах, радиоактивный распад и т.п.), либо микропрограмму.

Датчики случайных равномерно распределенных на интервале (0, 1) чисел имеются также во всех языках программирования высокого уровня (процедуры RANDOM).

В случае, когда таких датчиков нет, можно получить случайные числа программным способом. Наиболее часто для этого используют одно из рекуррентных соотношений:

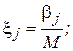
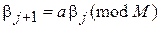, j =0,1,2,… (4)

где операция mod M означает остаток от деления 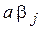на М; a и М – константы (положительные числа);

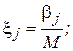
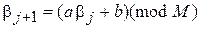, (5)

где b – положительное число.

Выбирая 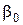, a, b и М, необходимо учитывать следующее:

1. Произведение 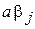в формуле (4) не должно быть кратным М. Иначе можно получить последовательность нулей. Для формулы (5) получение 0 не опасно. Поэтому для (4) 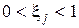, а для (5) .

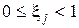2. Произведение 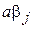в (4) или выражение 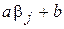в (5) не должны превышать максимально возможное для ЭВМ число, т.е.

; .

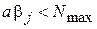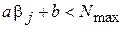В соответствии с алгоритмом получения случайных чисел

,

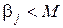поэтому должно быть

,

,

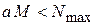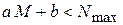откуда

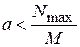для (4)

и

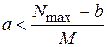для (5).

3. Полученные таким способом числа, строго говоря, не являются случайными, т.к. рекуррентный способ образования последовательности позволяет по известному числу этой последовательности (например, первому) однозначно определить все остальные. При этом не исключена возможность образования периодически повторяющихся циклов. Это объясняется тем, что при значениях

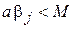
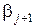ведет себя как показательная функция 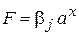, которая при достижении значения М скачком изменяется до нового начального значения 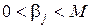и снова растет как 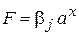до М.

В силу конечности М и рекуррентности алгоритма через некоторое время числа начнут повторяться.

При больших М и малых a период оказывается достаточно большим, например, при a = 23 и М = 10⁸ период 5 882 352 числа. В общем случае, период тем больше, чем больше М и меньше a. М определяет период повторения чисел, а a – степень случайности.

4. Если a много меньше М, а 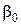малое, то в начале последовательности или там, где получилось малое очередное значение 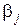, наблюдается неслучайный участок с последовательно возрастающими по закону 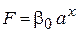числами, которые нельзя рассматривать случайными. Поэтому a должно быть достаточно большим, что противоречит требованию п. 3. Чтобы уменьшить длину этого участка, 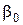следует брать примерно равным M/(5a).

Из–за этих причин получаемое распределение называют квазиравномерным, а числа последовательности – псевдослучайными.

При работе с целыми числами для обеспечения условий 1 – 4 принимают:

a – простое (нечетное) число (3, 5, 7, 11, 13, 17, 19, 23 и т.д.);

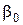– любое достаточно большое число;

М – четное не кратное a и достаточно большое число;

b – любое число, близкое .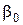

Функция плотности вероятностей равномерного распределения на интервале (a, b) имеет вид

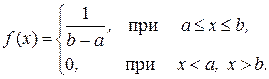
Математическое ожидание и дисперсия случайной величины x здесь равны

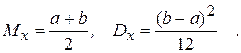
Для получения последовательности случайных чисел x_i, равномерно распределенных на интервале (a, b), следует воспользоваться формулой

,

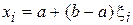где 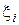– значение случайной величины, равномерно распределенной на интервале (0, 1).