Разность потенциалов на концах равновесной электрохимической цепи называется электродвижущей силой (эдс) и обозначается Е.

Электрохимическую цепь можно представить схематически. Например:

Cu | Zn | ZnS0₄ | CuS0₄ | Cu

Вертикальной сплошной чертой показывается наличие скачка потенциала на границе металл-металл, металл-раствор, а пунктирной - на границе двух растворов, так называемый диффузионный потенциал. Часто при записи цепи опускается повторение металла, предполагая, что цепь является правильно разомкнутой.

Разность потенциалов Е на концах этой цепи складывается из четырех гальвани-потенциалов, каждый из которых отдельно замерен быть не может:

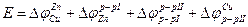
Полезная работа обратимого процесса (в данном случае электрическая) равна убыли энергии Гиббса, т.е.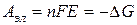

Для реакций, самопроизвольно протекающих в гальваническом элементе (∆G>0), эдс - положительна. Этому соответствует запись гальванического элемента так, чтобы правый электрод был более электроположителен, чем левый, движение электронов при этом происходит от левого электрода к правому, на котором и идет реакция восстановления.

На положительном электроде идет реакция восстановления, на отрицательном - окисления.

Эдс гальванического элемента можно рассчитывать по формуле Нернста:

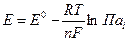(1)

где Е⁰- стандартная эдс цепи при активностях всех компонентов, равных единице; n - число электронов, участвующих в реакции; 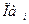- произведение активностей всех участников окислительно-восстановительной реакции в гальваническом элементе с учетом стехиометрических коэффициентов, которые для исходных веществ берутся со знаком «минус», а для продуктов «плюс».

Так, для приведенной выше гальванической цепи, где протекает реакция

CuS0₄ + Zn →ZnS0₄ + Сu,

ЭДС можно рассчитать по уравнению (1):

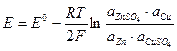
Комбинируя различные электроды между собой, можно получить множество электрохимических цепей. Поскольку измерить гальвани-потенциал невозможно, то за величину, характеризующую процесс на отдельном электроде, принимают электродный потенциал.