Уравнение изотермы химической реакции

При протекании химической реакции через некоторое время устанавливается равновесное состояние, когда скорости прямой и обратной реакции равны. Пусть в смеси идеальных газов протекает химическая реакция:

аА + вВ = eЕ + lL,

где а, в, е и l – число моль газообразных веществ А, В, Е и L, принимающих участие в реакции или стехиометрические коэффициенты.

Пусть в реакцию вступило бесконечно малое количество вещества А (dn_A); с ним прореагировало бесконечно малое количество вещества В (dn_B). В результате реакции образовалось dn_E и dn_L моль веществ С и D. Так как количество исходных веществ в ходе реакции убывает, а продуктов увеличивается, то величины dn_A и dn_B отрицательны, а dn_E и dn_L – положительны. Тогда изменение энергии Гиббса при протекании указанного процесса равно

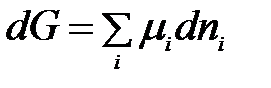
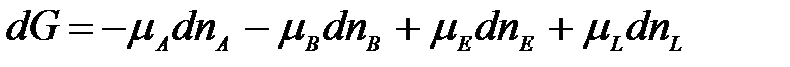
Выразим количества моль прореагировавших веществ dn_A, dn_B, dn_E, и dn_L через стехиометрические коэффициенты уравнения реакции. Согласно уравнению реакции:

с а моль вещества А реагирует в моль вещества В

с dn_A моль dn_B,

тогда

.

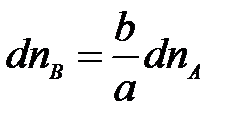Аналогично можно выразить:

;

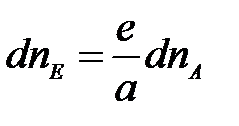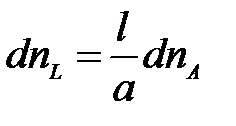
Подставим в уравнение для dG:

.

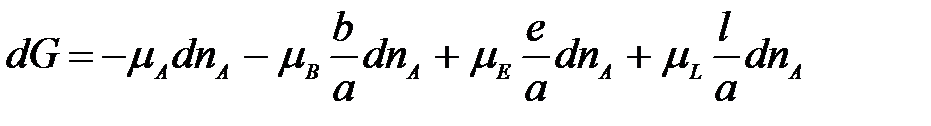Умножим левую и правую часть уравнения на а и поделим на dn_A:

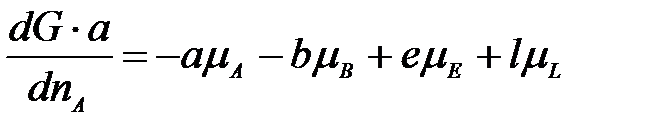
Так как химический потенциал равен мольной энергии Гиббса 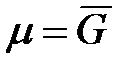, то

,

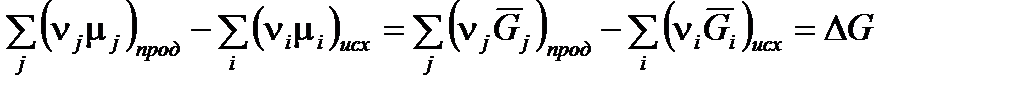следовательно,

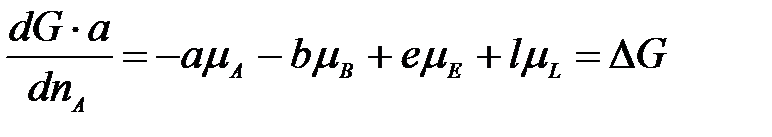
Химический потенциал компонента реакционной смеси равен

.

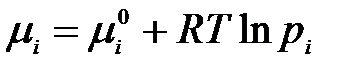Подставим в уравнение

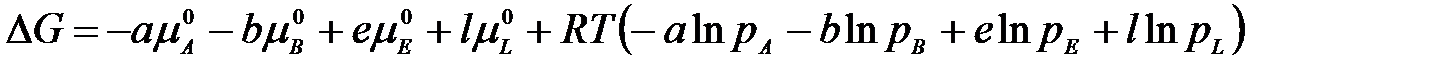
Обозначим сумму

,

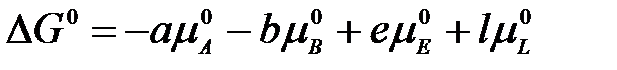Тогда

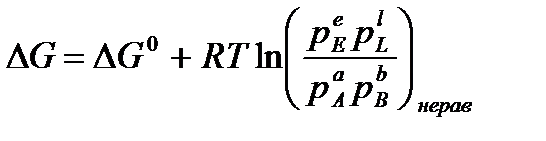. (3.1)

где ΔG⁰ – изменение энергии Гиббса в стандартных условиях; p_E, p_L, p_A, p_B – рабочие (неравновесные) парциальные давления компонентов в реакционной смеси.

Уравнение (3.1) называется уравнением изотермы химической реакции,

При постоянных давлении и температуре общим условием термодинамического равновесия является ΔG = 0. Тогда парциальные давления компонентов становятся равновесными 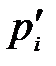и из уравнения (3.1) следует, что

.

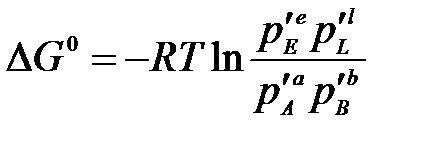Введем обозначение:

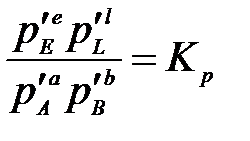, (3.2)

где К_р – термодинамическая константа равновесия – величина постоянная для данной реакции при данной температуре.

Термодинамическая константа равновесия является безразмерной величиной.

Полученное уравнение (3.2) выражает известный закон действия масс: отношение произведения равновесных парциальных давлений продуктов реакции, взятых в степенях, равных стехиометрическим коэффициентам к аналогичному произведению для исходных веществ при данной температуре есть величина постоянная.

С учетом К_р получим

,

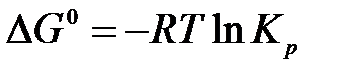тогда константу равновесия реакции можно рассчитать по уравнению:

.

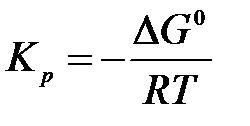К_р не зависит от давления, так как связана с изменением энергии Гиббса в стандартных условиях, т.е. при р = 1 атм.

Закон действия масс можно выразить не только через парциальные давления реагирующих веществ, но и через молярные концентрации (К_с) и мольные доли (К_х). Парциальное давление компонента системы связано с его молярной концентрацией и мольной долей уравнениями:

,

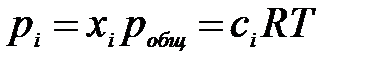где x_i – мольная доля i-го участника реакции; p_общ – общее давление реакционной смеси; с_i – молярная концентрация i-го участника реакции.

Тогда

;

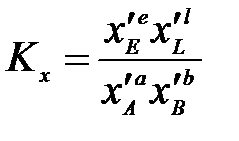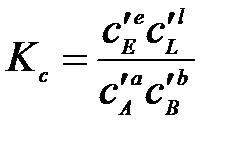
Константы К_х связаны К_р соотношением

,

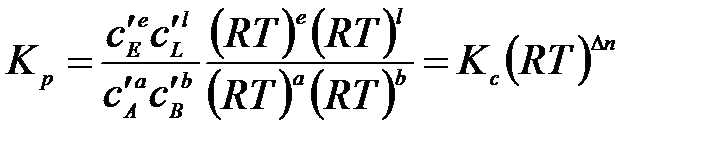где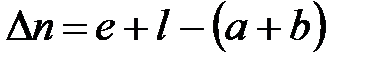

Аналогично

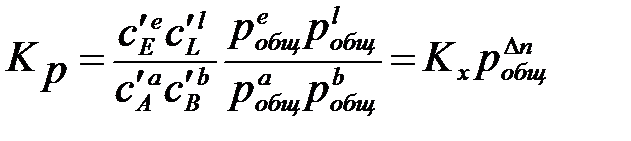
Константа K_x зависит от общего давления реакционной смеси.

Если реакция протекает в реальной системе, то вместо концентраций следует применять активности реагентов a_i, а вместо парциальных давлений – фугитивности:

;

,

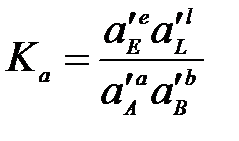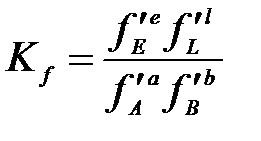где 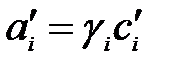- активность i-го участника реакции;

γ_i – коэффициент активности;

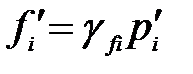- фугитивность (летучесть) i-го участника реакции;

γ_fi – коэффициент летучести.

Если химическая реакция протекает с участием конденсированных веществ (твердых или жидких), то химический потенциал таких веществ зависит только от температуры и при Т = const является постоянной величиной. Поэтому парциальные давления конденсированных веществ постоянны и входят в значение К_р, а закон действия масс записывается только для газообразных участников реакции. Например, для реакции

СаСО_3(тв) = СаО_(тв) + СО_2(г)

закон действия масс имеет вид

.

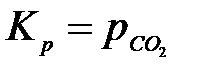Значения констант равновесия многих химических реакций при 298 К приведены в справочной литературе.