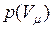I.3.2 ЭКСПЕРИМЕНТАЛЬНЫЕ ИЗОТЕРМЫ

Выводы, следующие из анализа уравнения Ван-дер-Ваальса, были подтверждены опытами ирландского учёного Т. Эндрюса, изучавшего изотермическое сжатие углекислого газа. Отличие экспериментальных и теоретических изотерм заключается в том, что превращению газа в жидкость в первом случае соответствуют горизонтальные участки, а во втором волнообразные.

Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая (рис.14), ограничивающая область двухфазных состояний вещества.

Рисунок 14 – Области равновесных состояний вещества на диаграмме

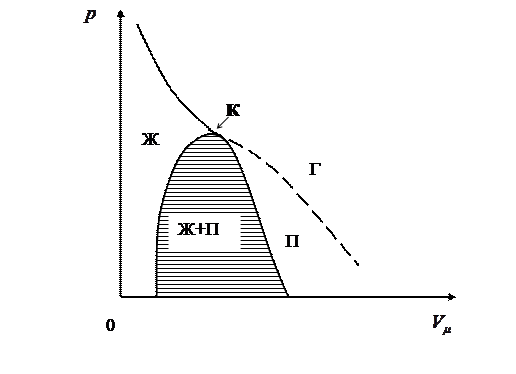
Эта кривая и критическая изотерма делят диаграмму р, 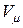под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от неё находится область жидкого состояния, а справа – область пара. Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же, при температуре выше критической не может быть превращён в жидкость ни при каком давлении. Сравнивая изотерму Ван–дер–Ваальса с изотермой Эндрюса (верхняя кривая на рис. 15), видим, что последняя имеет прямолинейный участок (2 – 6), соответствующий двухфазным состояниям вещества.

При некоторых условиях могут быть реализованы состояния, изображаемые участками ван-дер-ваальсовой изотермы (5–6) и (2–3). Эти неустойчивые состояния называются метастабильными. Участок (2-3) изображает перегретую жидкость , (5– 6) – пересыщенный пар. Обе фазы ограниченно устойчивы.

При достаточно низких температурах изотерма пересекает ось 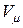, переходя в область отрицательных давлений (нижняя кривая на рис. 15). Вещество под отрицательным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок (8 - 9) на нижней изотерме соответствует перегретой жидкости, участок (9 – 10) – растянутой жидкости.

Рисунок 15 – Экспериментальные изотермы Эндрюса

Значения критических параметров 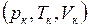выражаются через коэффициенты 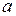и 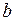в уравнении Ван-дер-Ваальса и универсальную газовую постоянную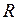

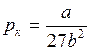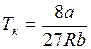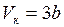, , . (I.75)