Полиномиальная аппроксимация
Применение рассмотренных методов исключения интервалов накладывает на функцию единственное требование – она должна быть унимодальной. Рассмотренные методы можно использовать для анализа как непрерывных, так и разрывных и дискретных функций. Их логическая структура основана на сравнении значений функции в двух пробных точках. При этом не учитывается величина разности между значениями функции.
Рассмотрим подход, который позволяет повысить эффективность определения экстремума за счет учета величины относительных изменений. Однако при этом на функцию накладываются дополнительные ограничения – она должна быть гладкой.
Основная идея состоит в возможности аппроксимации гладкой функции полиномами и использовании аппроксимирующего полинома для оценивания координаты точки экстремума.
Согласно теореме Вейерштрасса об аппроксимации, если функция непрерывна на некотором интервале, то ее с любой степенью точности можно аппроксимировать полиномом достаточно высокого порядка. Если для унимодальной функции найти такой полином, то его можно использовать для оценки точки экстремума функции.
Известно, что качество оценки точки экстремума можно повысить двумя путями:
· Повышением порядка полинома;
· Уменьшением интервала аппроксимации.
С точки зрения технологии второй метод является предпочтительным.
Простейшим вариантом полиномиальной аппроксимации является квадратичная аппроксимация, так как квадратичность хорошо сочетается с унимодальностью
Пусть заданы точки 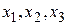 и соответствующие этим точкам значения функции
и соответствующие этим точкам значения функции 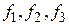 . Известно, что можно выбрать постоянные коэффициенты
. Известно, что можно выбрать постоянные коэффициенты 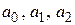 таким образом, что значения квадратичной функции
таким образом, что значения квадратичной функции
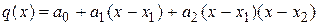 (2.3)
(2.3)
совпадут со значениями функции в трех указанных точках.
Примем, что в точке 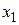 выполняется
выполняется 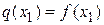 . Тогда
. Тогда
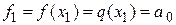 . Отсюда
. Отсюда 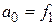 .
.
Коэффициент 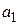 найдем из условия
найдем из условия 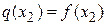 .
.
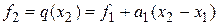 . Отсюда
. Отсюда 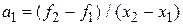 .
.
Наконец, из условия 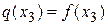 найдем
найдем 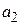 . Имеем
. Имеем
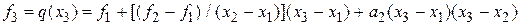 .
.
Решив последнее уравнение относительно 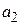 , получим
, получим
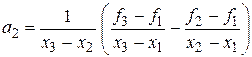 .
.
Если качество аппроксимации оказывается достаточно высоким, то оценку точки экстремума функции можно получить путем исследования стационарных точек полученного аппроксимирующего полинома.
Вычислим производную (2.3) и приравняем ее к нулю
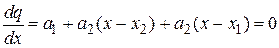 .
.
Отсюда 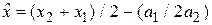 .
.
Пример. Найти оценку экстремальной точки для функции 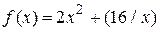 на интервале
на интервале 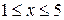 . Возьмем точки
. Возьмем точки 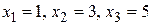 . Тогда
. Тогда 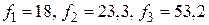 .
.
Найдем значения коэффициентов квадратичной аппроксимации:
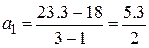 ,
,
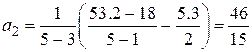 .
.
Подставив эти значения в формулу для 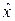 получим
получим 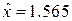 . Точное значение равно
. Точное значение равно 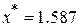 .
.
Дата добавления: 2020-03-17; просмотров: 1227;











