Метод золотого сечения
Минимаксные стратегии поиска диктуют следующие принципы:
· если количество пробных точек равно двум, их следует размещать на одинаковых расстояниях от середины интервала;
· пробные точки должны размещаться по симметричной схеме, чтобы отношение длины исключаемого подинтервала к исходному было постоянным;
· на каждой итерации процедуры поиска должно вычисляться только одно значение функции в вычисляемой точке.
Руководствуясь этими правилами, рассмотрим симметричное расположение точек, как это показано на рисунке 2.6.
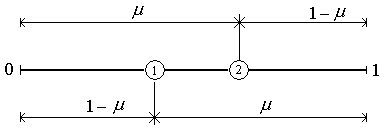
Рис. 2.6. Начальное расположение пробных точек в методе золотого сечения
Пробные точки стоят от граничных точек на расстоянии 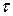 . При таком симметричном расположении точек длина остающегося интервала всегда равна
. При таком симметричном расположении точек длина остающегося интервала всегда равна 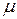 (рис.2.7)
(рис.2.7)
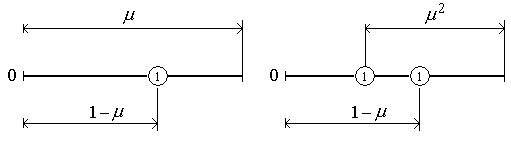
Рис. 2.7. Расположение пробных точек после первого шага исключения
Для того, чтобы симметрия поискового образа сохранялась, расстояние 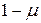 должно составлять
должно составлять 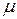 -ую часть длины интервала (которая равна
-ую часть длины интервала (которая равна 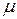 ). Это дает ношение
). Это дает ношение
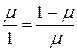 .
.
Отсюда можно получить квадратное уравнение 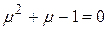 , положительное решение которого
, положительное решение которого 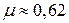 . Схема поиска, при котором пробные точки делят интервал в этом отношении, известна как метод золотого сечения. После каждой итерации исключается
. Схема поиска, при котором пробные точки делят интервал в этом отношении, известна как метод золотого сечения. После каждой итерации исключается 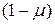 -ая часть от длины интервала. Следовательно, если исходный интервал имеет единичную длину, то длина интервала, полученного в результате
-ая часть от длины интервала. Следовательно, если исходный интервал имеет единичную длину, то длина интервала, полученного в результате 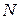 вычислений значений функции, будет равна
вычислений значений функции, будет равна 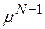 . Известно, что поиск с помощью метода золотого сечения является асимптотически наиболее эффективной реализацией минимаксной стратегии.
. Известно, что поиск с помощью метода золотого сечения является асимптотически наиболее эффективной реализацией минимаксной стратегии.
Рассмотрим прежний пример.Требуется минимизировать 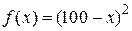 в интервале
в интервале 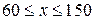 . Перейдем к интервалу единичной длины путем замены переменной по формуле
. Перейдем к интервалу единичной длины путем замены переменной по формуле 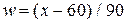 . Тогда задача принимает следующий вид:
. Тогда задача принимает следующий вид:
минимизировать 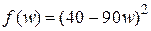 в интервале
в интервале 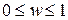 .
.
Итерация 1. 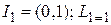 . Проведем два первых вычисления функции:
. Проведем два первых вычисления функции:
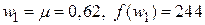 ,
,
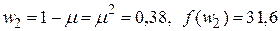 .
.
Так как 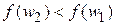 , интервал
, интервал 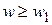 исключается.
исключается.
Итерация 2. 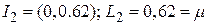 . Следующее вычисление функции проводится в точке
. Следующее вычисление функции проводится в точке
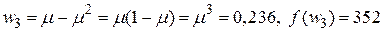 ,
,
Так как 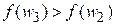 , интервал
, интервал 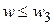 исключается.
исключается.
В результате двух итераций остался интервал 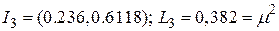 .
.
В процессе расчетов проведено 3 вычисления функции 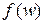 . Длина результирующего интервала для переменной
. Длина результирующего интервала для переменной 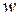 равна
равна 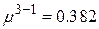 . Если пересчитать на переменную
. Если пересчитать на переменную 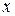 , то длина интервала
, то длина интервала 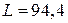 .
.
Дата добавления: 2020-03-17; просмотров: 771;











