Безусловная оптимизация функции нескольких переменных

Подавляющее число реальных задач оптимизации, представляющих практический интерес, являются многомерными: в них целевая функция зависит от нескольких аргументов, причем, иногда их число может быть весьма большим.

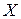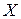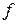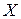Математическая постановка таких задач аналогична их постановке в одномерном случае: ищется наименьшее (наибольшее) значение целевой функции, заданной на некотором множестве возможных значений ее аргументов. В случае, когда целевая функция непрерывна, а множество является замкнутой ограниченной областью, остается справедливой теорема Вейерштрасса о существовании глобального минимума функции на . Тем самым, выделяется класс задач оптимизации, для которых гарантировано существование решения. В дальнейшем мы всегда будем предполагать, не оговаривая этого особо, что все рассматриваемые задачи принадлежат этому классу.

Как и в одномерном случае, характер задачи и соответственно возможные методы решения существенно зависят от той информации о целевой функции, которая нам доступна в процессе ее исследования. В одних случаях целевая функция задается аналитической формулой, являясь при этом дифференцируемой функцией. Тогда можно вычислить ее частные производные, получить явное выражение для градиента, определяющего в каждой точке направления возрастания и убывания функции, и использовать эту информацию для решения задачи. В других случаях никакой формулы для целевой функции нет, а имеется лишь возможность определить ее значение в любой точке рассматриваемой области (с помощью расчетов, в результате эксперимента и т. д.). В таких задачах в процессе решения мы фактически можем найти значения целевой функции лишь в конечном числе точек, и по этой информации требуется приближенно установить ее наименьшее значение для всей области.

Многомерные задачи, естественно, являются более сложными и трудоемкими, чем одномерные, причем, обычно, трудности при их решении возрастают при увеличении размерности.

Как и в случае одной переменной сначала рассмотрим задачу анализа, связанную с классификацией точек пространства нескольких переменных. Задача звучит так: соответствуют ли исследуемые точки решениям многомерной задачи безусловной оптимизации, в которой требуется найти экстремум функции 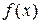, при отсутствии ограничений на 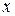, где 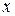- вектор управляемых переменных размерности 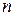, 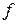- скалярная целевая функция.

Будем считать, что функция 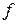и ее производные существуют и всюду непрерывны. Это позволяет использовать для разработки конструктивных критериев оптимизации понятие градиента

.

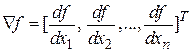Вектор градиента дает общее представление о поведении функции в окрестности точки 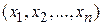. Обычно, в литературе, для обозначения градиента используется символ « 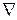- набла», либо обозначение «grad». Направление этого вектора является направлением наиболее быстрого возрастания функции в данной точке. Противоположное ему направление, которое часто называют антиградиентным, представляет собой направление наиболее быстрого убывания функции. Модуль градиента определяет скорость возрастания и убывания функции в направлении градиента и антиградиента. Для всех остальных направлений скорость изменения функции в точке 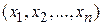меньше модуля градиента. При переходе от одной точки к другой как направление градиента, так и его модуль, вообще говоря, меняются.

Градиентные методы требуют вычисления градиента целевой функции на каждом шаге. Если она задана аналитически, то это, как правило, не проблема: для частных производных, определяющих градиент, можно получить явные формулы. В противном случае частные производные в нужных точках приходится вычислять приближенно, заменяя их соответствующими разностными отношениями.