Метод Ньютона-Рафсона

Пусть функция 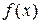дважды дифференцируема. И пусть у нас есть возможность найти аналитическое выражение для 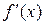. Работа алгоритма начинается в точке начального приближения 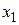, которая представляет собой начальное приближение стационарной точки функции 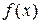или корня уравнения 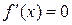(рис.2.8).

Рис. 2.8. Графическое представление метода Ньютона-Рафсона

Затем строится линейная аппроксимация функции 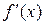в точке 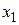(проводится касательная до пересечения с осью 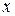). Точка, в которой аппроксимирующая прямая обращается в нуль, принимается в качестве следующего приближения.

Линейная функция, аппроксимирующая функцию 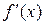в точке , записывается в виде

.

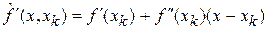Приравняв правую часть к нулю, получим следующее приближение

.

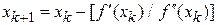Пример. Минимизировать функцию 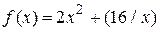на интервале 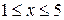. Воспользуемся методом Ньютона-Рафсона, положив . Имеем

, .

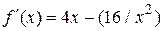Итерация 1.

, , , .

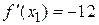Итерация 2.

, , , .

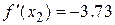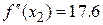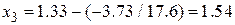Итерации продолжаются до тех пор, пока не будет выполняться неравенство 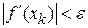, где 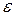- заранее установленная величина допустимого отклонения.