Метод средней точки
Если имеется возможность вычислять как значения самой функции, так и ее производной, то для нахождения корня уравнения 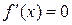 можно воспользоваться эффективным алгоритмов исключения интервалов, на каждой итерации которого рассматривается лишь одна пробная точка. Если в точке
можно воспользоваться эффективным алгоритмов исключения интервалов, на каждой итерации которого рассматривается лишь одна пробная точка. Если в точке 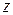 выполняется неравенство
выполняется неравенство 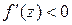 , то с учетом унимодальности естественно утверждать, что точка минимума не может лежать левее точки
, то с учетом унимодальности естественно утверждать, что точка минимума не может лежать левее точки 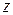 . Соответственно интервал
. Соответственно интервал 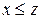 может быть исключен. И наоборот, если в точке
может быть исключен. И наоборот, если в точке 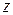 выполняется неравенство
выполняется неравенство 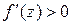 , то естественно утверждать, что точка минимума не может лежать правее точки
, то естественно утверждать, что точка минимума не может лежать правее точки 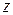 .
.
Определим две точки 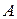 и
и 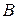 таким образом, что
таким образом, что 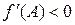 и
и 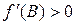 .Тогда стационарная точка расположена между
.Тогда стационарная точка расположена между 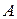 и
и 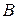 . Вычислим производную в средней точке рассматриваемого интервала
. Вычислим производную в средней точке рассматриваемого интервала 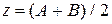 . Если
. Если 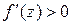 , то интервал
, то интервал 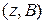 можно исключить из интервала поиска. Если
можно исключить из интервала поиска. Если 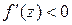 , то интервал
, то интервал 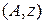 можно исключить из интервала поиска.
можно исключить из интервала поиска.
Логическая структура поиска в соответствии с изложенным методом исключения интервалов основана лишь на исследовании знака производной, независимо от значений, которые эта производная принимает.
Метод секущих
Метод секущих, являющийся комбинацией метода Ньютона и общей схемы исключения интервалов, ориентирован на нахождение корней уравнения 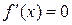 в интервале
в интервале 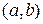 , если такой корень существует.
, если такой корень существует.
Предположим, что в точках 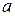 и
и 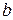 знаки производной различны (рис.2.9). Аппроксимируем функцию
знаки производной различны (рис.2.9). Аппроксимируем функцию 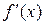 секущей прямой, соединяющей точки
секущей прямой, соединяющей точки 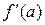 и
и 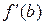 и найдем точку, в которой секущая графика
и найдем точку, в которой секущая графика 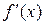 пересекает ось абсцисс. Определим уравнение секущей по обычной методике.
пересекает ось абсцисс. Определим уравнение секущей по обычной методике.
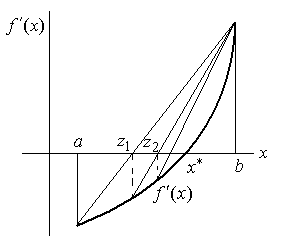
Рис. 2.9. Иллюстрация метода секущих
Пусть заданы точки 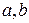 и соответствующие этим точкам значения функции
и соответствующие этим точкам значения функции 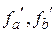 . Известно, что секущую можно записать как
. Известно, что секущую можно записать как
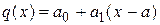 .
.
Коэффициенты 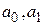 находятся из условий
находятся из условий
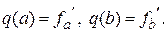
Тогда 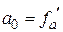 ,
, 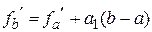 и уравнение для нахождения точки пересечения с осью абсцисс имеет вид
и уравнение для нахождения точки пересечения с осью абсцисс имеет вид
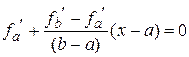 .
.
Отсюда следующее приближение к точке 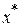 определяется по формуле
определяется по формуле
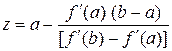 .
.
Пример. Требуется минимизировать функцию 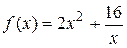 на интервале
на интервале 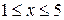 . Найдем первую производную
. Найдем первую производную 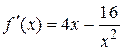 .
.
Итерация 1.
Шаг 1. 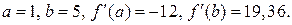
Шаг 2. 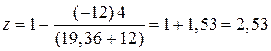 .
.
Шаг 3. 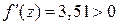 . Поскольку знак производной в новой точке положителен, отбрасываем интервал
. Поскольку знак производной в новой точке положителен, отбрасываем интервал 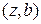 и принимаем
и принимаем 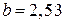 . Значение производной в новой точке
. Значение производной в новой точке 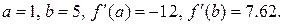
Итерация 2.
Шаг 2. 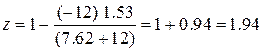 .
.
Шаг 3. 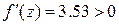 . Производная опять положительна, поэтому корректируем правый конец интервала. Принимаем
. Производная опять положительна, поэтому корректируем правый конец интервала. Принимаем 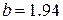 .
.
Дата добавления: 2020-03-17; просмотров: 1052;











