Прямые методы поиска экстремума функции одной переменной

Рассматривая вопросы классификации методов поиска экстремума функции (методов оптимизации), мы рассматривали такой показатель, как объем необходимой информации для реализации метода. По этому признаку мы выделили

· прямые методы (методы нулевого порядка), требующие только вычислений целевой функции в точках приближений;

· методы первого порядка: требуют вычисления первых частных производных функции;

· методы второго порядка: требуют вычисления вторых частных производных целевой функции.

Ясно, что разные методы предъявляют различные требования к гладкости и наличию у целевой функции частных производных

Начнем с методов первого типа, реализующих поиск точки экстремума внутри заданного интервала. Прежде всего, мы сосредоточимся на методах, которые позволяют определить экстремум функции одной переменной путем последовательного уменьшения интервала поиска. Эти методы носят название методов исключения интервалов.

Ранее нами было дано определение унимодальной функции. Фактически все методы поиска, используемые на практике, предполагают, что на интервале поиска функция обладает свойством унимодальности. Полезность этого свойства состоит в том, что для унимодальной функции сравнение значений функции в двух точках интервала позволяет определить, в каком из двух заданных двумя указанными точками подинтервалов точка экстремума отсутствует.

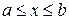Теорема.Пусть функция унимодальна на замкнутом интервале , а ее минимум достигается в точке 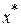(рис.2.5). Рассмотрим точк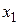и и 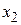, расположенные на интервале таким образом, что 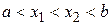. Сравнивая значения функции в точках 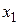и 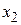, можно сделать следующие выводы.

· Если 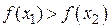, то точка минимума не лежит в интервале 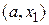, т.е. .

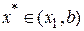· Если 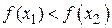, то точка минимума не лежит в интервале 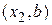, т.е. .

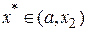· Если 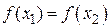то можно исключить оба крайних интервала 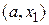и .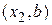

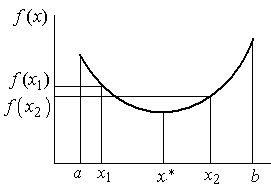
Рис. 2.5 Иллюстрация к методам исключения интервалов

На основе такого алгоритма можно реализовать процедуру поиска, которая будет сводиться к последовательному исключению частей исходного интервала. Достоинством такого подхода является то, что он основан только на вычислении значений самой функции. При этом не требуется ее дифференцируемость. Более того, допустимы даже случаи, когда функцию нельзя записать аналитически. Тем более этот метод применим к разрывным и дискретным функциям.

Будем считать, что для функции определен интервал изменения переменной, на котором выполняются условия унимодальности. Тогда значение точки экстремума может быть получено путем сжатия интервала за счет отбрасывания подинтервалов. Величина отбрасываемого подинтервала зависит от размещения пробных точек. Выбор точек желательно делать так, чтобы уменьшение интервала на каждом шаге было максимальным и количество вычислений функции было минимальным.

Существует большое число алгоритмов уменьшения интервала. Некоторые из них изложены ниже, с другими можно познакомиться по литературе [2,3,4,6], а также при выполнении лабораторных работ.