Метод деления отрезка пополам

Данный метод позволяет исключить в точности половину интервала на каждой итерации. Иногда его называют трехточечным поиском на равных интервалах

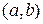Пусть функция задана на интервале . Метод можно представить в виде следующей последовательности шагов.

Шаг 1. Положить 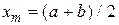и 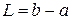. Вычислить .

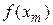Шаг 2. Положить 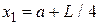и 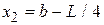. В результате точки 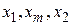делят интервал 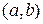на четыре равные части. Вычислить 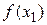и .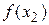

Шаг 3. Сравнить 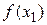и .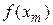

Если 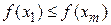, исключить интервал 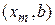, положив 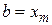. Средней точкой нового интервала становится точка 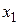. Следовательно, необходимо положить 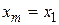. Перейти к шагу 6.

Если 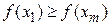, перейти к шагу 4.

Шаг 4. Если 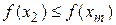, исключить интервал 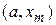, положив 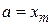. Средней точкой нового интервала становится точка 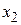. Следовательно, необходимо положить 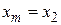. Перейти к шагу 6.

Шаг 5. Убрать два крайних интервала, положив , .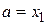

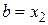Шаг 6. Вычислить 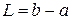. Если величина 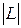мала, закончить поиск. Иначе, вернуться к шагу 2.

Таким образом:

· На каждой итерации исключается в точности половина интервала поиска.

· Средняя точка последовательно получаемых интервалов всегда совпадает с одной из пробных точек 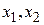или 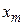, что уменьшает число вычислений.

· Если проведено 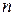вычислений значений функции, то длина полученного интервала составляет 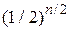величины исходного интервала.

Пример.Требуется минимизировать 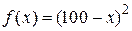в интервале 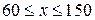. Здесь .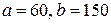

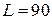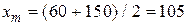
Итерация 1

,

,

,

.

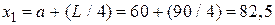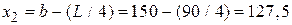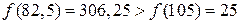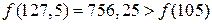Таким образом, исключаются интервалы 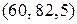и 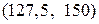. Длина интервала поиска уменьшается с 90 до 45.