Статистическое распределение выборки
Пусть из генеральной совокупности извлечена выборка, причем значение х1 наблюдалось п1 раз, х2 наблюдалось п2 раз, …, хк наблюдалось пк раз. Общий объем выборки можно определить как
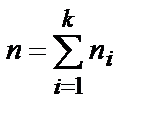 .
.
Наблюдаемые значения хi называют вариантами, а последовательность вариант, записанных в возрастающем порядке, – вариационным рядом.
Числа наблюдений называют частотами, а их отношения к объему выборки 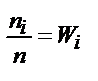 – относительными частотами.
– относительными частотами.
Модой М0называется варианта, имеющая наибольшую частоту.
Медианой Мe называется варианта, которая делит вариационный ряд на две части с одинаковым числом вариант в каждой.
Для дискретного вариационного ряда с нечетным числом членов медиана равна серединной варианте, а для ряда с четным числом членов – полусумме двух серединных вариант.
Размахом выборки называется разность между максимальным и минимальным элементами выборки.
Статистическим распределением выборки (статистическим рядом) называют перечень вариант и соответствующих им частот или относительных частот.
| xi | x1 | x2 | … | xk |
| ni | n1 | n2 | … | nk |
или
| xi | x1 | x2 | … | xk |
| wi | w1 | w2 | … | wk |
Статистическое распределение можно задать также в виде последовательности интервалов одинаковой длины и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
| х | х0– х1 | х1 – х2 | … | хк-1– хк |
| пi | п1 | п2 | … | пк |
В таком виде под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.
Дата добавления: 2018-11-26; просмотров: 850;











