Закон распределения вероятностей дискретной случайной величины

Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.

Каждое значение дискретной случайной величины имеет определенную вероятность появления. Пусть возможное значение x₁ наступает с вероятностью p₁, значение x₂ – с вероятностью p₂ и т.д.

Законом распределениявероятностей дискретной случайной величины X называется любое правило, позволяющее находить все вероятности вида .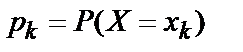

Простейшей формой задания закона распределения дискретной случайной величины Х является таблица, которая состоит из двух строк. В первой строке записываются все возможные значения случайной величины, а во второй – вероятности появления этих значений:

X			…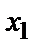
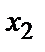
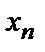
P			…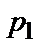

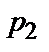
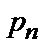
Здесь .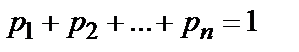

Закон распределения дискретной случайной величины можно изобразить графически. В прямоугольной системе координат строят точки M₁(x₁, p₁), M₂(x₂, p₂), ..., M_n(x_n, p_n) (x_i – возможные значения случайной величины X, p_i – соответствующие вероятности) и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения (рис. 1) или полигоном распределения вероятностей.

Рис. 10.1 Многоугольник распределения вероятностей

Многоугольник распределения, так же как и ряд распределения, полностью характеризует случайную величину.