Эмпирическая функция распределения. Полигон частот и гистограмма
Предположим, чтополучено статистическое распределение выборки. Обозначим через nx число наблюдений, при которых значения вариант оказываются меньше, чем x.
Эмпирической функцией распределения случайной величины (функцией распределения выборки) называют функцию 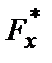 относительной частоты числа наблюдений nx:
относительной частоты числа наблюдений nx:
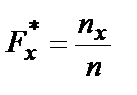 ,
,
т.е. относительной частоты события X<x.
Наглядное представление о статистическом распределении выборки дают графики.
Полигоном частот называют ломаную (рис. 11.1), отрезки которой соединяют точки 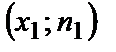 ,
, 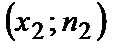 , …,
, …, 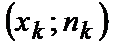 . Для построения полигона частот на оси абсцисс откладывают варианты
. Для построения полигона частот на оси абсцисс откладывают варианты 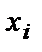 , а на оси ординат – соответствующие им частоты
, а на оси ординат – соответствующие им частоты 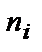 . Точки
. Точки 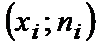 соединяют отрезками прямых и получают полигон частот.
соединяют отрезками прямых и получают полигон частот.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки 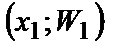 ,
, 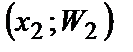 , …,
, …, 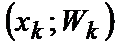 . Для построения полигона относительных частот на оси абсцисс откладывают варианты
. Для построения полигона относительных частот на оси абсцисс откладывают варианты 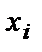 , а на оси ординат – соответствующие им относительные частоты
, а на оси ординат – соответствующие им относительные частоты 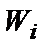 . Точки
. Точки 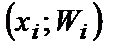 соединяют отрезками прямых и получают полигон относительных частот.
соединяют отрезками прямых и получают полигон относительных частот.
Полигон обычно строят для дискретного признака.

Рис. 11.1 Полигон частот
В тех случаях, когда рассматривается непрерывная случайная величина, которая может принимать любые, сколь угодно мало отличающиеся друг от друга значения, строится не полигон, а гистограмма. Для этого весь интервал, в котором заключены все значения случайной величины, разбивается на несколько интервалов длиной h каждый. На этих интервалах подсчитывается сумма частот вариант, попавших в i-й интервал, и составляется отношение 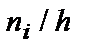 .
.
Гистограммой частот называют ступенчатую фигуру (рис. 11.2), состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 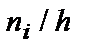 (плотность частоты).
(плотность частоты).

Рис. 11.2 Гистограмма частот
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии 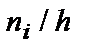 . Площадь i-го частичного прямоугольника равна
. Площадь i-го частичного прямоугольника равна 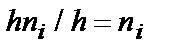 – сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
– сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 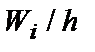 (плотность относительной частоты).
(плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии 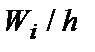 . Площадь i-го частичного прямоугольника равна
. Площадь i-го частичного прямоугольника равна 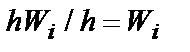 – относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме относительных частот, т.е. единице.
– относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме относительных частот, т.е. единице.
Пример.Имеется выборка, содержащая 30 числовых значений некоторого признака случайной величины Х:
| Построить: 1) статистическое распределение выборки; 2) полигон частот; 3) эмпирическую функцию распределения; 4) интервальный ряд; 5) гистограмму частот; | вычислить: 6) выборочную среднюю; 7) выборочную дисперсию; 8) выборочное среднее квадратическое отклонение; 9) моду; 10) медиану. |
Решение.
1. Статистическое распределение выборки представляет собой таблицу, в которой первая строка содержит варианты (значения случайной величины, расположенные в порядке возрастания), а вторая – соответствующие частоты (сколько раз эти значения встречались).
| хi | ||||||||||
| ni |
2. Полигон частот – это ломаная, соединяющая точки с координатами (хi; ni).
3. Проведем вычисления для построения эмпирической функции распределения:
| Если х ≤ 14, то | 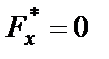
|
| если 14 < х ≤ 16, то | 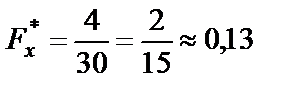
|
| если 16 < х ≤ 17, то | 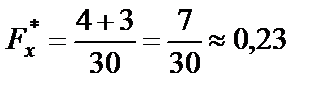
|
| если 17 < х ≤ 18, то | 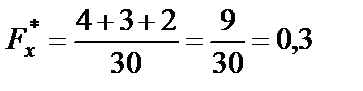
|
| если 18 < х ≤ 19, то | 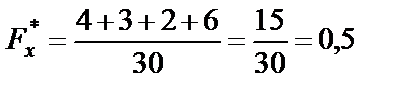
|
| если 19 < х ≤ 20, то | 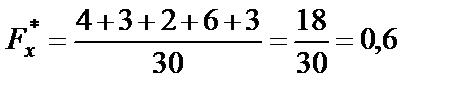
|
| если 20 < х ≤ 22, то | 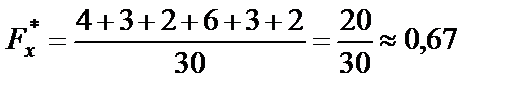
|
| если 22 < х ≤ 24, то | 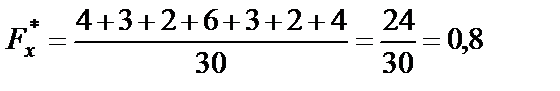
|
| если 24 < х ≤ 25, то | 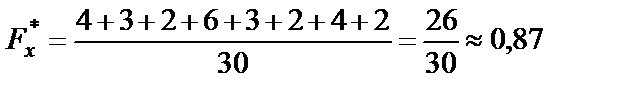
|
| если 25 < х ≤ 26, то | 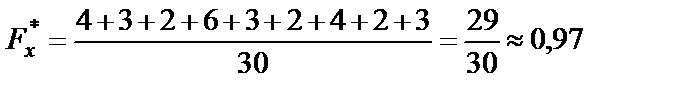
|
| если х > 26, то | 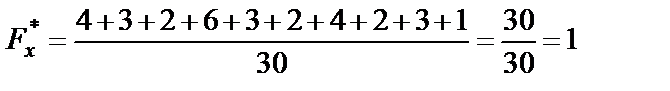
|
Получили эмпирическую функцию распределения:

4. Построим интервальный ряд.
Найдем наименьшее и наибольшее значения признака в совокупности и определим размах варьирования: R=xmax–xmin=26–14=12.
Определим число интервалов k. Для этого воспользуемся формулой Стерджесса:
k =1+3,322∙lgn = 1+3,322∙lg30 ≈ 6.
Найдем постоянную величину интервала: 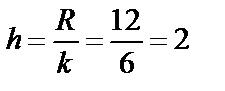 .
.
Определим границы интервалов. За начало первого интервала следует взять х0=х min=14. Промежуточные интервалы получаем, прибавляя к концу предыдущего интервала длину частичного интервала h=2:
х1=14+2=16, х2 =16+2=18, х3=18+2=20, х4=20+2=22, х5=22+2=24, х6=24+2=26. Будем рассматривать следующие промежутки: [14; 16], (16; 18], (18; 20], (20; 22], (22; 24], (24; 26] и посчитаем количество вариант для каждого промежутка.
Получим статистическое распределение интервального ряда:
| хi | 14 –16 | 16 – 18 | 18 – 20 | 20 – 22 | 22 – 24 | 24 – 26 |
| ni |
5. Построим гистограмму частот:
6. Вычислим характеристики ряда. Статистическое распределение ряда, вычисленное выше (пункт 1), имеет вид:
| хi | ||||||||||
| ni |
Выборочная средняя:
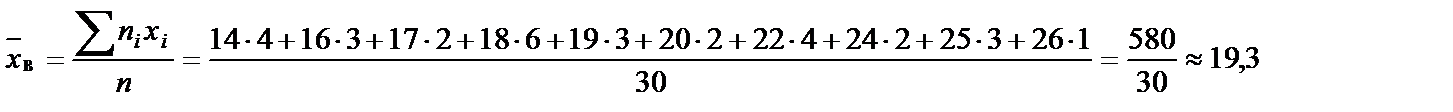
7. Выборочная дисперсия:
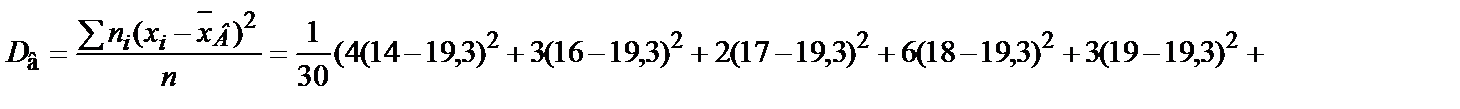
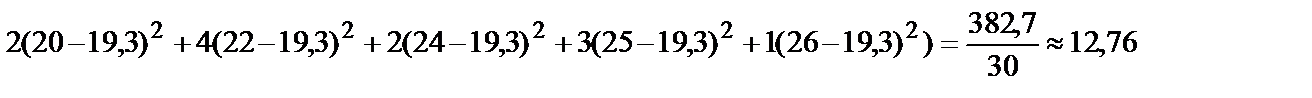 .
.
8. Среднее квадратическое отклонение: 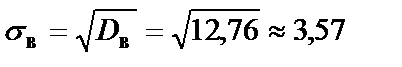 .
.
9. Запишем вариационный ряд (все значения в порядке возрастания):
14, 14, 14, 14, 16, 16, 16, 17, 17, 18, 18, 18, 18, 18, 18, 19, 19, 19, 20, 20, 22, 22, 22, 22, 24, 24, 25, 25, 25, 26
Мода –наиболее часто встречаемое значение, М0 = 18.
10. Медиана – варианта, которая делит вариационный ряд на две части с одинаковым числом вариант в каждой. Для нашего ряда с четным числом членов – медиана равна полусумме двух серединных вариант.
14, 14, 14, 14, 16, 16, 16, 17, 17, 18, 18, 18, 18, 18, 18, 19, 19, 19, 20, 20, 22, 22, 22, 22, 24, 24, 25, 25, 25, 26
Медиана Мe 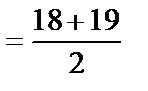 = 18,5.
= 18,5.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Письменный Д.Т. Конспект лекций по высшей математике. В 2 ч. / Д.Т. Письменный – 3-е изд. – М.: Айрис-пресс, 2005. 1 ч. – 288 с.
2. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Часть 1: Учеб. Пособие для втузов / Данко П.Е., Попов А.Г., Кожевникова Т.Я. – М.:ОНИКС, 2005. – 304 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман – М.: Высшая школа, 2004. – 479 с.: ил.
4. Кремер Н.Ш. Теория вероятностей и математическая статистика / Н.Ш. Кремер – М.: ЮНИТИ – ДАНА, 2004. – 573с.
5. Лунгу К.Н Сборник задач по высшей математике. 2 курс / К.Н. Лунгу, В.П. Норин., Д.Т. Письменный, Ю.А. Шевченко; под ред. С.Н. Федина. – М.: Айрис-пресс, 2004. – 592 .: ил.
6. Гусак А.А. Теория вероятностей: справ. пособ. к решению задач / А.А. Гусак, Е.А. Бричикова. – 6-е изд. – Минск: ТетраСистемс, 2007. – 288 с.
7. Шапкин А.С. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями: Учебное пособие / А.С. Шапкин, В.А Шапкин. – 7-е изд., – М.: Издательско-торговая корпорация «Дашков и Ко», 2010. – 432 с.
8. Киселева Н.Г. Системный анализ и моделирование экосистем: конспект лекций / Н.Г. Киселева. – Йошкар-Ола: Марийский государственный технический университет, 2008. – 128 с.
9. Киселева Н.Г. Математические методы обработки данных: метод. указания для практ. и самост. работ. – Казань: Изд-во Казанского ГАУ, 2016. – 54с.
10. Киселева Н.Г. Теория вероятностей и математическая статистика: Учебно-методические пособие. Казанский ГАУ. Н.Г. Киселева, А.Н. Зиннатуллина, С.Р. Еникеева, Казань, 2014. – 128 с.
Дата добавления: 2018-11-26; просмотров: 2452;











