Числовые характеристики непрерывных случайных величин
Если все возможные значения случайной величины 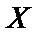 принадлежат интервалу
принадлежат интервалу 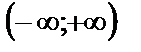 , то числовые характеристики непрерывной случайной величины находят по формулам:
, то числовые характеристики непрерывной случайной величины находят по формулам:
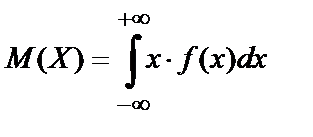 ,
, 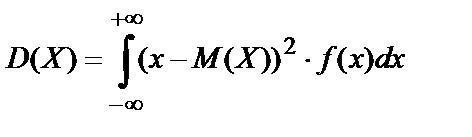 (10.27)
(10.27)
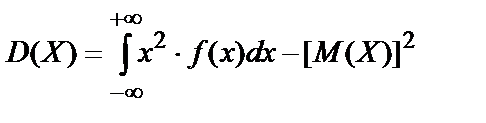 ,
, 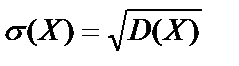 . (10.28)
. (10.28)
Если все возможные значения случайной величины 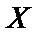 принадлежат конечному интервалу
принадлежат конечному интервалу 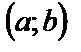 , то пределы интегрирования в приведенных выше формулах заменяются соответственно
, то пределы интегрирования в приведенных выше формулах заменяются соответственно 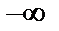 на
на 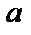 ,
, 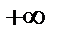 на
на 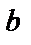 .
.
Все свойства математического ожидания и дисперсии для дискретных случайных величин переносятся и на случай непрерывных случайных величин.
Пример 1.Найти математическое ожидание, дисперсию исреднее квадратическое отклонение случайной величины Х, если известен ее закон распределения:
| X | –1 | |||
| P | 0,3 | 0,2 | 0,4 | 0,1 |
Решение.
1. Математическое ожидание 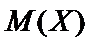 вычисляем по формуле:
вычисляем по формуле:
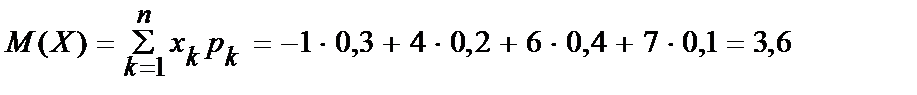 .
.
2. Дисперсию вычислим по формуле:
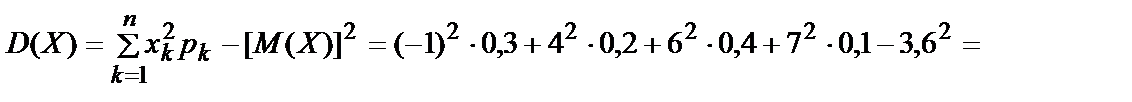 9,84.
9,84.
3. Среднее квадратическое отклонение вычисляем по формуле:
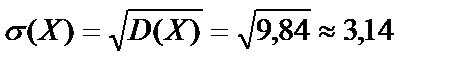 .
.
Пример 2.Дискретная случайная величина задана законом распределения вероятностей:
| X | |||
| P | 0,3 | 0,5 | 0,2 |
Найти функцию распределения вероятностей и построить ее график.
Решение.
По формуле
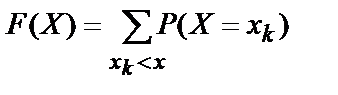
получаем:
если 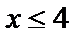 , то
, то 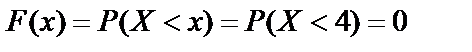 ;
;
если 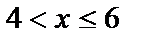 , то
, то 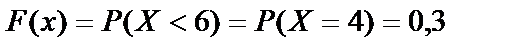 ;
;
если 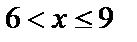 , то
, то 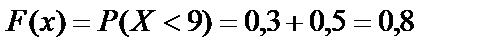 ;
;
если 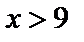 , то
, то 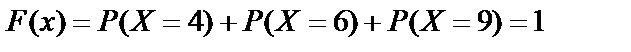 .
.
Искомая функция распределения имеет вид

Построим график этой функции:
| X |
| F(x) |
| 0,3 |
| 0,8 |
Пример 3.Непрерывная случайная величина задана функцией распределения вероятностей F(x). Требуется: а) найти плотность распределения вероятностей f(x); б) найти математическое ожидание, дисперсию, среднее квадратическое отклонение; в) построить графики функции распределения F(x) и плотности распределения f(x).
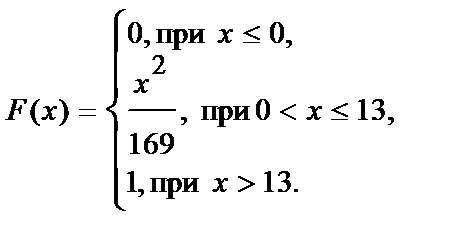
Решение.
1. Плотность распределения вероятностей
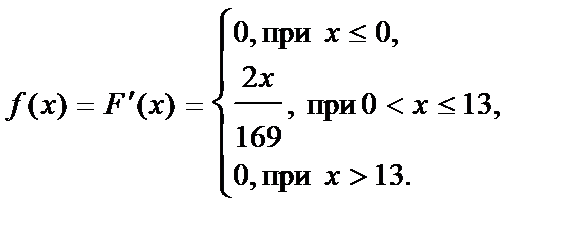
2. Математическое ожидание
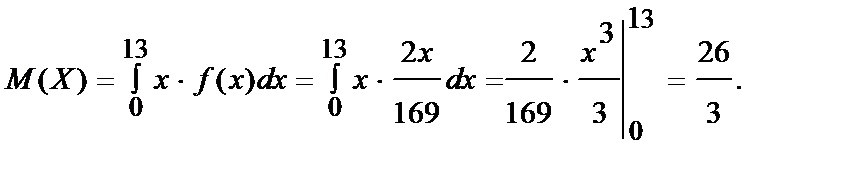
3. Дисперсия
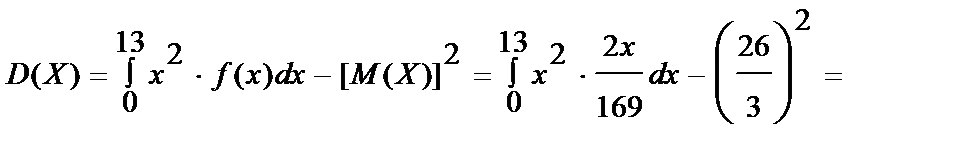
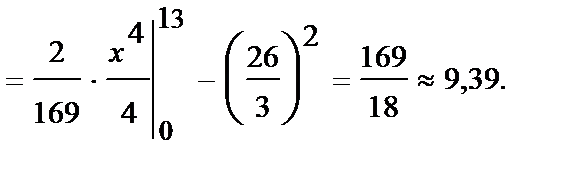
4. Среднее квадратическое отклонение
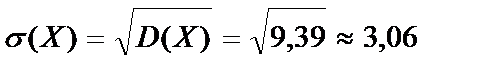 .
.
5. График функции распределения F(x):
График плотности распределения f(x):
Дата добавления: 2018-11-26; просмотров: 930;











