Плотность распределения вероятностей непрерывной случайной величины
Плотностью распределения непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):
f(x)=F'(x) (10.25)
Из этого определения следует, что функция распределения является первообразной для плотности распределения.
Заметим, что для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.
Свойства плотности распределения:
10. Плотность распределения – неотрицательная функция: 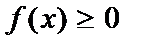 , т.к. F(x) – неубывающая функция.
, т.к. F(x) – неубывающая функция.
20. Вероятность того, что непрерывная случайная величина 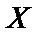 примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 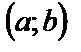 , определяется равенством:
, определяется равенством:
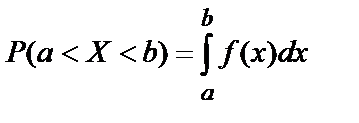 . (10.26)
. (10.26)
Геометрически – это значит, что вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу 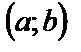 , равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f (x) и прямыми х = а, х = b.
, равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f (x) и прямыми х = а, х = b.
30. Несобственный интеграл от плотности распределения в пределах от –∞ до +∞ равен единице:
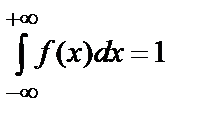 .
.
Геометрически – это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и кривой распределения, равна единице.
Частный случай. Если все возможные значения случайной величины принадлежат интервалу 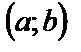 , то
, то
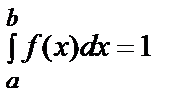 .
.
Дата добавления: 2018-11-26; просмотров: 852;











