Функция распределения случайной величины
Непрерывную случайную величину нельзя охарактеризовать перечнем всех ее возможных значений и их вероятностей. Естественно, встает вопрос о том, нельзя ли охарактеризовать случайную величину иным способом, одинаково годным как для дискретных, так и для непрерывных случайных величин.
Функция распределения является универсальной характеристикой случайной величины, т.к. полностью характеризует случайную величину с вероятностной точки зрения, то есть является одной из форм закона распределения.
Функцией распределения вероятностейназывают функцию F(x), определяемую формулой:
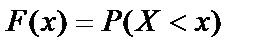 . (10.24)
. (10.24)
Свойства функции распределения:
10. Значения функции распределения принадлежат отрезку [0;1]:
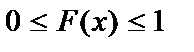 .
.
20. Функция распределения есть неубывающая функция:
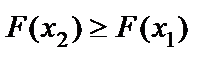 , если
, если 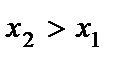 .
.
Следствие 1. Вероятность того, что случайная величина X примет значение, заключенное в промежутке (a; b), равна приращению функции распределения на этом интервале:
P(a<X<b)=F(b)–F(a).
Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, например x1, равна нулю: P(X=x1)=0.
30. Если все возможные значения случайной величины X принадлежат интервалу (a; b), то
F(x)=0 при 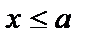 ; F(x)=1 при
; F(x)=1 при 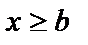 .
.
Следствие. Справедливы следующие предельные соотношения:
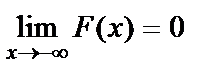 ,
, 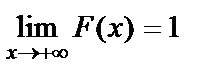 .
.
Функция распределения дискретной случайной величины является кусочно-постоянной функцией со скачками в точках, являющихся значениями случайной величины; величины скачков равны вероятностям, с которыми эти значения принимаются, т.е. если 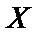 –дискретная случайная величина, то
–дискретная случайная величина, то 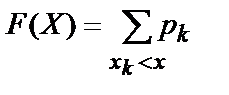 .
.
Дата добавления: 2018-11-26; просмотров: 836;











