Формула полной вероятности. Формула Бейеса
Формула полной вероятности. Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий 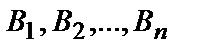 , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A.
, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A.
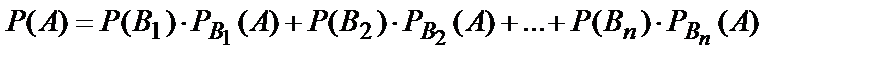 . (10.14)
. (10.14)
Формула Бейеса. Пусть событие A может наступить лишь при условии появления одного из несовместных событий (гипотез) 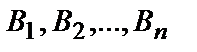 , которые образуют полную группу событий. Если событие A уже произошло, то условная вероятность любой гипотезы
, которые образуют полную группу событий. Если событие A уже произошло, то условная вероятность любой гипотезы 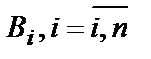 может быть вычислена по формуле:
может быть вычислена по формуле:
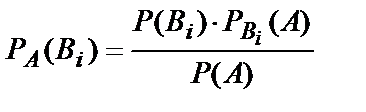 , (10.15)
, (10.15)
где Р(А)– формула полной вероятности.
Если производятся испытания, при которых вероятность появления события A в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события A.
Пример 1. В группе из 10 студентов, пришедших на экзамен, 3 подготовлено отлично, 4 – хорошо, 2 – посредственно и 1 плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный – на 16, посредственно – на 10, плохо – на 5. Найти вероятность того, что вызванный наугад студент ответит на три произвольно заданных вопроса.
Решение.
A – студент ответит на три произвольно заданных вопроса;
B1 – студент подготовлен отлично;
B2 – студент подготовлен хорошо;
B3 – студент подготовлен посредственно;
B4 – студент подготовлен плохо.
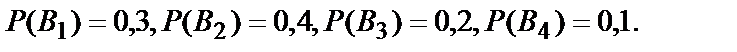
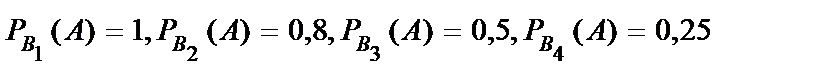 .
.
По формуле полной вероятности (10.14):
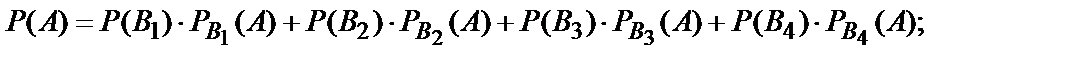
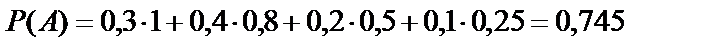 .
.
Пример 2.В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:4:5. Практика показала, что телевизоры, поступающие от 1-го, 2-го и 3-го поставщиков, не потребуют ремонта в течение гарантийного срока соответственно в 98%, 88% и 92% случаев. Найти вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока.
Решение.
A – телевизор не потребует ремонта в течение гарантийного срока;
B1 – телевизор поступил в торговую фирму от 1-го поставщика;
B2 – телевизор поступил в торговую фирму от 2-го поставщика;
B3 – телевизор поступил в торговую фирму от 3-го поставщика.
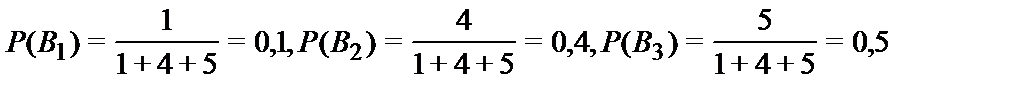
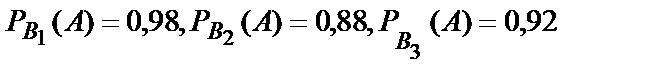 .
.
По формуле полной вероятности (10.14):
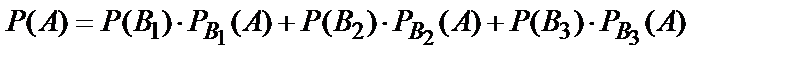 ;
;
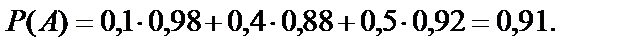
Пример 3.Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата в 5 раз больше производительности второго. I автомат производит в среднем 75 % деталей отличного качества, а II автомат – 87 %. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что деталь произведена II автоматом.
Решение.
A – деталь отличного качества;
B1 – деталь произведена первым автоматом;
B2 – деталь произведена вторым автоматом.
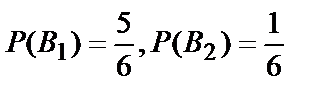 ;
; 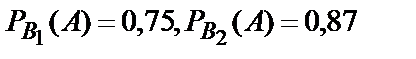 .
.
Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности (10.14) равна
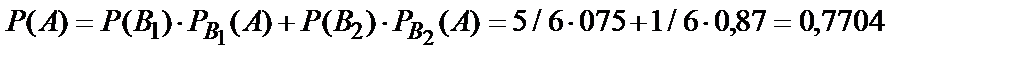 .
.
Искомая вероятность того, что взятая отличная деталь произведена вторым автоматом, по формуле Бейеса (10.15) равна
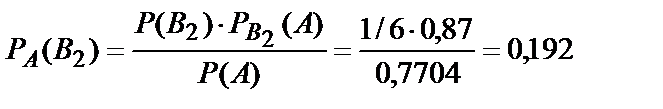 .
.
Пример 4. Имеются три одинаковые урны: I урна содержит 1 белый и 6 черных шаров, II – 3 белых и 2 черных шаров, III – 7 белых и 8 черных шаров. Из наудачу выбранной урны вынут шар. Он оказался белым. Чему равна вероятность того, что шар вынут из I урны?
Решение.
A –вынут белый шар;
B1 – выбрана I урна;
B2 – выбрана II урна;
B3 – выбрана III урна.
| 1бел 6чер | 3бел 2чер | 7бел 8чер |
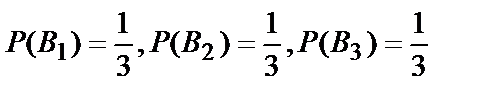 ;
;
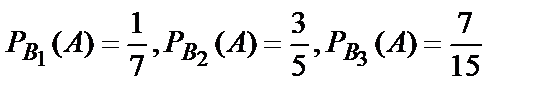 .
.
По формуле полной вероятности (10.14):
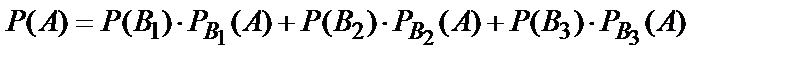 .
.
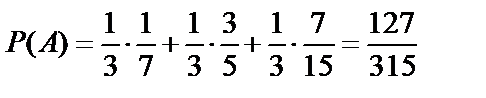 .
.
Искомая вероятность по формуле (10.15) равна:
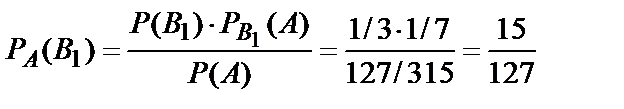 .
.
Дата добавления: 2018-11-26; просмотров: 1170;











